|
QM-Methoden » Statistik » Grundlagen |
Druckversion |
Statistische Methoden im Qualitätsmanagement
Einerseits existieren zu diesem Thema zahlreiche Bücher mit tausenden von Seiten. Andererseits gibt es umfangreiche Statistiksoftware, die dem Anwender Lösungen für seine Probleme anbietet sowie das Nachschlagen in Tabellen und Rechnen erspart.
Referenzhandbücher zu Qualitätsstandards enthalten ausführliche Anleitungen zur Ermittlung der Fähigkeit von Messystemen (MSA, VDA 5) oder zur Bestimmung der Prozessfähigkeit (VDA 3).
Daher werden hier lediglich gemeinsame Konzepte für die Methoden erläutert, die in den folgenden Seiten detaillierter behandelt werden.
Streuung
Misst man die Ergebnisse von hinreichend komplexen Prozessen, die mit einem festen Komplex von Bedingungen wiederholt ablaufen, stellt man fest, dass die Ergebnisse nicht exakt gleich sind. Da der feste Komplex von Bedingungen nicht alle Bedingungen umfasst, die einen Einfluss auf das Ergebnis haben, tritt eine Streuung auf.
Ursachen der Streuung können unterteilt werden nach:
- Mensch
- Maschine
- Material
- Methode
- Umwelt
Daher ist das Ergebnis eines einzelnen Versuches nicht vorhersagbar. Die Menge der Ergebnisse einer großen Zahl von Versuchen unterliegt jedoch Gesetzmäßigkeiten.
Als Grundlage für die folgenden Seiten, die einzelne statistische Methoden behandeln, sind die folgenden Inhalte geplant:
- Wahrscheinlichkeit
- Verteilungen
- Schätzen und Testen
-
Einfluss auf eine Zielgröße
- Fehlerfortpflanzung
- Varianzanalyse
- Regression
Wahrscheinlichkeit
Die Wahrscheinlichkeit p1 för ein Ereignis E1 ist eine Maßzahl, die angibt, mit welcher relativen Häufigkeit E1 im Verhältnis zu Ω auftritt.
Dabei ist E1 = {e1, e2, e3,..., en} die Menge der Elementarereignisse e, bei deren Eintreten wir das Ereignis E1 registrieren. Ω = {e1, e2, e3,..., em}; m > n ist die Menge aller im betrachteten Umweltausschnitt möglichen Elementarereignisse. Elementarereignisse sind Ergebnisse von gedachten oder tatsächlichen Zufallsexperimenten, die sich gegenseitig ausschließen.
Elementarereignisse sind beispielsweise die Augenzahlen eines Würfels. Betrachten wir die Wahrscheinlichkeit eine 6 zu würfeln, ist E6 = {6} und Ω = {1, 2, 3, 4, 5, 6}. Da wir bei einem Würfel voraussetzen, dass alle Elementarereignisse gleich wahrscheinlich sind, können wir hier E6 über die klassische Definition der Wahrscheinlichkeit, Zahl der günstigen Fälle dividiert durch Zahl der möglichen Fälle berechnen und erhalten 1/6. Diese Voraussetzung machen wir auch, wenn wir die Wahrscheinlichkeit berechnen, bei einer Prüfung ein fehlerhaftes Produkt zu finden.
Wenn unsere Elementarereignisse dagegen Ankünfte von Mitarbeitern zur Arbeit in festgelegten Zeitabschnitten sind, können wir nicht mehr von gleicher Wahrscheinlichkeit der Elementarereignisse ausgehen.
Wahrscheinlichkeiten erfüllen einige Bedingungen:
- Wahrscheinlichkeiten sind nicht negativ: p ≥ 0
- Wahrscheinlichkeiten sind nicht größer als 1: p ≤ 1
- Die Wahrscheinlichkeit, dass entweder das Ereignis E1 oder das Ereignis E2 eintritt, ist gleich der Summe der Eintrittswahrscheinlichkeiten dieser Ereignisse, sofern die Ereignisse sich gegenseitig ausschließen.
Der Additionssatz
Wir fragen nach der Wahrscheinlichkeit, dass entweder das Ereignis E1 oder das Ereignis E2 eintritt. Dabei unterscheiden wir zwei Fälle:
Die Ereignisse schließen sich gegenseitig aus.
![]() Dieser Fall wurde bereits bei den Bedingungen, die Wahrscheinlichkeiten
erfüllen müssen, behandelt.
Dieser Fall wurde bereits bei den Bedingungen, die Wahrscheinlichkeiten
erfüllen müssen, behandelt.
Beispiel 1
Es wird mit einem Würfel gewürfelt. Gefragt wird nach der Wahrscheinlichkeit entweder eine 1 oder eine 6 zu würfeln.
E1 = {1} E2 = {6} P = p1+ p2 = 1/6 + 1/6 = 1/3
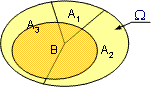
Die Ereignisse schließen sich nicht aus.
![]() In
der Mengenkreisdarstellung repräsentiert die gesamte gefärbte Fläche die
Wahrscheinlichkeit, dass Ereignis 1 oder Ereignis 2
eintritt. Denkt man sich die überlappenden Mengenkreise aus den beiden nicht
überlappenden Mengenkreisen des Beispiels 1 gebildet, wird klar, dass bei der Addition der Wahrscheinlichkeiten die überlappende Fläche doppelt gezählt wird. Sie muss daher einmal abgezogen werden,
um das richtige Ergebnis zu erhalten.
In
der Mengenkreisdarstellung repräsentiert die gesamte gefärbte Fläche die
Wahrscheinlichkeit, dass Ereignis 1 oder Ereignis 2
eintritt. Denkt man sich die überlappenden Mengenkreise aus den beiden nicht
überlappenden Mengenkreisen des Beispiels 1 gebildet, wird klar, dass bei der Addition der Wahrscheinlichkeiten die überlappende Fläche doppelt gezählt wird. Sie muss daher einmal abgezogen werden,
um das richtige Ergebnis zu erhalten.
Beispiel 2
Es wird mit 2 Würfeln gewürfelt. Gefragt wird nach der Wahrscheinlichkeit entweder mit Würfel 1 eine 3 oder mit Würfel 2 eine 4 zu würfeln.
E1 = {W1: 3} E2 = {W2: 4} P = p1 + p2 - p(E1 ∩ E2)
In diesem Fall gilt p(E1 ∩ E2) = p1 * p2. Und damit:
P = 1/3 - 1/36 = 0,306
Der Multiplikationssatz
Hier fragen wir nach der Wahrscheinlichkeit, dass die Ereignisse E1 und E2 gemeinsam auftreten. In Beispiel 2 haben wir dafür bereits eine Lösung gefunden. Denn die Schnittmenge von E1 und E2 repräsentiert ja den Fall, dass wir mit Würfel 1 eine 3 und mit Würfel 2 eine 4 gewürfelt haben. Wir müssen allerdings unterscheiden:
Die Ereignisse sind statistisch unabhängig.
Beispiel 3
Es wird mit 2 Würfeln gewürfelt. Gefragt wird nach der Wahrscheinlichkeit mit Würfel 1 eine 3 und mit Würfel 2 eine 4 zu würfeln.
E1 = {W1: 3} E2 = {W2: 4} P = p(E1 ∩ E2)
In diesem Fall gilt p(E1 ∩ E2) = p1 * p2. Und damit:
P = 1/36 = 0,028
Die Ereignisse sind statistisch abhängig.
Beispiel 4
 Es
wird mit einem Würfel gewürfelt. Gefragt wird nach der Wahrscheinlichkeit, dass das Resultat eine
gerade Zahl und eine Zahl > 3 ist.
Es
wird mit einem Würfel gewürfelt. Gefragt wird nach der Wahrscheinlichkeit, dass das Resultat eine
gerade Zahl und eine Zahl > 3 ist.
E1 = {2,4,6} E2 = {4,5,6} P = p(E1 ∩ E2)
(E1 ∩ E2) = {4,6} p(E1 ∩ E2) = 1/3 = 0,333
Dies ist verschieden von dem Ergebnis, das man durch Multiplikation von p1 und p2 erhalten würde. Der Grund dafür ist die statistische Abhängigkeit zwischen E1 und E2. Wenn das Ereignis E1, eine gerade Augenzahl, eintritt, ist mit einer Wahrscheinlichkeit von 2/3 auch E2, eine Zahl größer 3, gegeben, weil von den drei Elementarereignissen, die in E1 vorhanden sind, zwei auch zu E2 gehören.
Statistische Unabhängigkeit, bedingte Wahrscheinlichkeit
Eine Lösung für Beispiel 4 erhalten wir auch, wenn wir sagen: Die Wahrscheinlichkeit, dass E1 und E2 eintreten, ist gleich der Wahrscheinlichkeit, dass E1 eintritt, multipliziert mit der Wahrscheinlichkeit, dass E2 eintritt, nachdem E1 bereits eingetreten ist.
Als Formel geschrieben:
p(E1 ∩ E2) = p(E1)*p(E2 | E1)
p(E1 | E2) wird als bedingte Wahrscheinlichkeit des Ereignisses E2 unter der Bedingung E1 bezeichnet.
Bei Beispiel 4 ist p(E1) = 1/2 und, wie wir bereits erläutert hatten, p(E2 | E1) = 2/3. Damit ergibt sich für p(E1 ∩ E2) wiederum das Ergebnis 1/3.
Gehen wir zurück auf Beispiel 3, sehen wir, dass die Augenzahl des zweiten Würfels durch die des ersten nicht beeinflusst wird. p(E2 | E1) ist hier also einfach gleich p(E2).
Die Bedingung für statistische Unabhängigkeit können wir also durch
p(E1 ∩ E2) = p(E1)*p(E2)
formulieren. Dies ist einerseits eine Rechenvorschrift: Wenn wir wissen oder annehmen, dass zwei Ereignisse unabhängig sind, können wir die Schnittmenge berechnen.
Andererseits erlaubt die Formel auch einen Test: Wenn wir Wahrscheinlichkeiten für die Ereignisse und für die Schnittmenge haben, können wir feststellen, ob die Ereignisse unabhängig sind.
Beispiel 5
30% der beanstandeten Rechnungen wiesen Rechenfehler (E1) auf. Bei 20% waren Leistungen falsch ausgewiesen (E2). 15% der Rechnungen enthielten beide Fehler nebeneinander. Sind die Fehler statistisch unabhängig?
p(E1)*p(E2) = 0,3*0,2 = 0,06 < 0,15 = p(E1 ∩ E2)
Sofern die Stichprobe, an der die Wahrscheinlichkeiten ermittelt wurden, ausreichend groß war, sind die beiden Fehlerarten nicht statistisch unabhängig. Sie weisen eine Korrelation auf. Möglicherweise haben sie eine gemeinsame Ursache. Daher sollten sie bei einer Problemlösung gemeinsam betrachtet werden.
Totale Wahrscheinlichkeit und Bayessche Formel
Hat man in einem Ereignisfeld Ω ein vollständiges System von n Ereignissen Ai, i = 1, 2, 3, ..., n so dass gilt:
 A1 ∪ A2 ∪ A3 ∪ ...An = Ω Ai ∩ Aj = Ø
A1 ∪ A2 ∪ A3 ∪ ...An = Ω Ai ∩ Aj = Ø
In diesem Ereignisfeld ist ein weiteres Ereignis B definiert, das mindestens mit einem Ai eine nicht leere Schnittmengen bildet, so dass weiter gilt:
B = B∩(A1 ∪ A2 ∪ A3 ∪ ...An)
Da die Ai sich gegenseitig ausschließen, schließen sich auch die B ∩ Ai aus, und man erhält für die Wahrscheinlichkeit von B (Totale Wahrscheinlichkeit):
P(B) = ∑ P(B | Ai) * P(Ai)
Aus der Definition der bedingten Wahrscheinlichkeit folgt, dass P(B | Ai) * P(Ai) = P(Ai | B) * P(B). Löst man dies nach P(Ai | B) auf und ersetzt P(B) mit Hilfe der totalen Wahrscheinlichkeit gelangt man zur Formel von Bayes:
P(Ai | B) = P(B | Ai) * P(Ai) / ∑ P(B | Ai) * P(Ai)
Die Formel für die totale Wahrscheinlichkeit enthält 2n + 1 Variable und gestattet es also, wenn 2n experimentell ermittelt sind, die fehlende Variable zu berechnen. Die Bayessche Formel erlaubt den Sichtwechsel von B | Ai auf Ai | B. In beiden Fällen können Informationen, die direkt nur schwer zu erhalten sind, aus anderen, leichter zugänglichen, durch Rechnung ermittelt werden.
Beispiel 6
Eine Weinkellerei bietet in verschiedenen Getränkemärkten einige Weine des neuen Jahrgangs zum Probieren an. Darunter befindet sich auch ein nach einem neuartigen Verfahren ausgebauter Wein. Die Testtrinker können den Gesamteindruck bewerten mit:
- A1: Vorzüglich
- A2: Gut
- A3: Weniger gut
Das Ereignis B wird dadurch repräsentiert, dass der nach dem neuartigen Verfahren hergestellte Wein getestet wurde.
Die Weinkellerei erhält das folgende Ergebnis, das lediglich den Anteil des nach dem neuen Verfahren hergestellten Weins in den verschiedenen Kategorien angibt.:
| Beurteilung | Stimmen | Neues Verfahren |
|---|---|---|
| Vorzüglich | 220 | 55% |
| Gut | 670 | 24% |
| Weniger gut | 380 | 35% |
Interessant ist natürlich die Frage, mit welchem Prozentsatz der nach dem neuen Verfahren hergestellte Wein in die drei Kategorien eingestuft wird. Dies wird nach der Formel von Bayes berechnet:
P(A1 | B) = 0,55*220/(0,55*220+0,24*670+0,35*380) = 0,29
Die Summe der Stimmen tritt im Zähler und Nenner auf und wird deswegen gekürzt
Analoge Rechnung für die anderen Bewertungen führt zu dem Ergebnis:
- Vorzüglich: 29%
- Gut: 39%
- Weniger gut: 32%
Das Baumdiagramm
Das Baumdiagramm ist eine einfache und übersichtliche Möglichkeit, die Wahrscheinlichkeiten von aufeinanderfolgenden Ereignissen zu berechnen.
Das Baumdiagramm beginnt an einem Ursprung O. Für jede Wahlmöglichkeit wird ein Pfad eingezeichnet, der an einem Knotenpunkt endet. Der Knotenpunkt entspricht einem Ereignis. Er kann entweder Ausgangspunkt für weitere Pfade oder ein Endpunkt sein. Für die Auswertung von Baumdiagrammen gelten die folgenden Regeln:
- Multiplikationsregel: Verläuft der Pfad zu einem Endknoten über mehrere Zwischenknoten, erhält man die Wahrscheinlichkeit des Ereignisses, das durch den Endknoten repräsentiert wird, durch die Multiplikation der Wahrscheinlichkeiten der einzelnen Pfade, aus denen sich der zu dem Endknoten führende Pfad zusammensetzt.
- Additionsregel: Wird ein Ereignis durch mehrere Endknoten, die über verschiedene Pfade erreicht werden, repräsentiert, ist die Wahrscheinlichkeit des Ereignisses gleich der Summe der Wahrscheinlichkeiten, mit denen die zugehörigen Endknoten erreicht werden.
- Ergänzung zu 1: Die Wahrscheinlichkeiten, mit denen die Endknoten erreicht werden, ergänzen sich zu 1.
 Beispiel 7
Beispiel 7
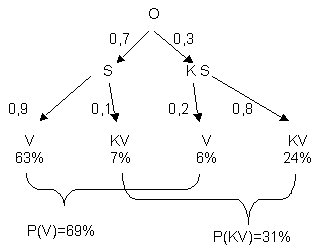
Ein Qualitätsmanager schätzt seine Chancen auf eine erfolgreiche Teilnahme an einer Schulung in statistischen Methoden auf 0,7. Die Wahrscheinlichkeit, nach der Schulung die Auswertung der vorhandenen Qualitätsaufzeichnungen deutlich zu verbessern, schätzt er auf 0,9. Ohne die Schulung glaubt er die verbesserte Auswertung jedoch nur mit einer Wahrscheinlichkeit von 0,2 durchführen zu können.
Um herauszufinden, wie wahrscheinlich die Verbesserung ist, zeichnen wir ein Baumdiagramm. Darin bedeuten:
S: Schulung KS: Keine Schulung V: Verbesserung KV: Keine Verbesserung
Zu der Gesamtwahrscheinlichkeit von 69% für die Verbesserung trägt die Verbesserung nach Schulung 63% bei. Die Verbesserungswahrscheinlichkeit ist eine bedingte Wahrscheinlichkeit, die von der Schulung offensichtlich statistisch abhängig ist.
Kombinatorik
In vielen praktischen Fällen haben die Elementarereignisse in einem Ereignisfeld bekannte Wahrscheinlichkeiten:
- Kopf beim Münzwurf
- Würfeln einer 6 mit einem Würfel
- Entnehmen eines defekten Teils aus einer Stichprobe mit dem Fehleranteil x%
Die Kombinatorik erlaubt es, daraus Wahrscheinlichkeiten für Ereignisse, die nach festgelegten Regeln aus den Elementarereignissen gebildet werden, zu berechnen. Weil gleich wahrscheinliche Elementarereignisse betrachtet werden, ist die Wahrscheinlichkeit gleich der Zahl der günstigen Fälle dividiert durch die Zahl der möglichen Fälle. Viele derartige Ereignisse lassen sich durch ein Urnenmodell simulieren
Zur Erläterung betrachten wir die Frage, wie groß die Wahrscheinlichkeit dafür ist, dass wir bei der Entnahme einer Stichprobe von 4 Teilen aus einer Grundgesamtheit, die 25% Ausschuss enthält, 0, 1, 2, 3 oder 4 defekte Teile erhalten.
Das Urnenmodell dazu ist eine Urne mit n=4 Kugeln, von denen eine schwarz (defekt) ist und die anderen drei weiss (intakt) sind. Aus dieser Urne ziehen wir nach Mischen eine Kugel, notieren die Farbe und legen die Kugel zurück. Dies wiederholen wir, bis wir vier Kugeln gezogen haben. Wie groß ist nun die Wahrscheinlichkeit, dass wir gerade k mal die schwarze Kugel ziehen?
Beispiel 8
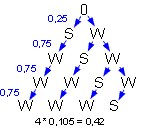 Als Beispiel betrachten wir den Fall, dass k=1 ist. Zur Berechnung der Wahrscheinlichkeit verwenden wir ein vereinfachtes Baumdiagramm, das nur die Zweige enthält, die zu dem gewünschten Ergebnis k=1 führen.
Als Beispiel betrachten wir den Fall, dass k=1 ist. Zur Berechnung der Wahrscheinlichkeit verwenden wir ein vereinfachtes Baumdiagramm, das nur die Zweige enthält, die zu dem gewünschten Ergebnis k=1 führen.
Offensichtlich gibt es vier Pfade zu dem gewünschten Ereignis, die sich nur durch die Reihenfolge, in der die schwarze und die weißen Kugeln gezogen werden, unterscheiden. Daher erhalten wir als Wahrscheinlichkeit für diesen Fall:
P(1;4) = 4 * 0,251 *0,753 = 0,42
Da es zwar ohne weiteres möglich ist, nach der beschriebenen Methode auch die Wahrscheinlichkeiten für die anderen Fälle zu berechnen, der Weg über das Baumdiagramm für größere Modelle jedoch zu umständlich ist, untersuchen wir unser Ergebnis genauer. Die möglichen Reihenfolgen, in denen die schwarze und die weißen Kugeln gezogen werden sind gemäß dem Baumdiagramm:
| S | W | W | W |
| W | S | W | W |
| W | W | S | W |
| W | W | W | S |
Dies entspricht der Vertauschung (Permutation) von 4 Elementen. Hierfür gibt es 4! Möglichkeiten. Da wir aber die Vertauschungen der weißen Kugeln untereinander nicht als neuen Zustand sehen, müssen wir dies durch die Zahl der Permutationen der weißen (und der schwarzen) Kugeln dividieren und erhalten:
P(1;4) = 4!/(1!*3!) * 0,251 *0,753
Oder verallgemeinert die Wahrschinlichkeit unter n gezogenen Kugeln mit Zurücklegen k schwarze zu erhalten:
P(k;n) = n!/(k!*(n-k)!) * pk *(1-p)(n-k)
Dabei ist p die Wahrscheinlichkeit eine schwarze Kugel zu ziehen. Dies entspricht der Zahl der schwarzen Kugeln dividiert durch die Gesamtzahl der Kugeln in der Urne.
n!/(k!*(n-k)!) wird als Kombination von n zur k-ten Klasse bezeichnet.
Verteilungen
Verteilungen beschreiben die Wahrscheinlichkeit von Ereignissen mathematisch. Sofern die Verteilungsfunktion für eine Zufallsvariable, deren Ausprägung ein Ereignis aus der Menge der möglichen Ereignisse repräsentiert, bekannt ist, kann die Wahrscheinlichkeit aller möglichen Ereignisse berechnet werden.
Diskrete Verteilungen
Eine diskrete Verteilung liegt vor, wenn die Zufallsvariable nur bestimmte, beispielsweise ganzzahlige Werte annehmen kann.
Die Verteilungsfunktion ist gegeben durch:
F(x) = P(X ≤ x)
Sie gibt die Wahrscheinlichkeit dafür an, dass die Zufallsvariable X einen Wert kleiner oder gleich x annimmt.
Für die Augenzahl eines Würfels ergibt sich die Verteilungsfunktion:
![]()
![]()
Dies ist eine Treppenkurve, die die Werte 1/6 bis 1 durchläuft. 1/6 ist die Wahrscheinlichkeit, dass ein Wert x auftritt. Bezeichnen wir diese mit f(xi), kann die Verteilungsfunktion allgemein geschrieben werden:
![]()
f(xi) ist die Wahrscheinlichkeitsfunktion.
Wichtige Kenngrößen einer Verteilung sind der Erwartungswert μ und die Varianz σ2.
Erwartungswert:
![]()
Varianz:
![]()
Die Wurzel aus der Varianz ist die Standardabweichung σ. Für Stichproben der Größe n entspricht dem Erwartungswert der Mittelwert:
![]()
Die Varianz wird nach
![]()
berechnet.
Wie groß sind der Erwartungswert und die Varianz für die Augenzahl eines Würfels?
Binomialverteilung
Die Binomialverteilung gibt Antwort auf die Frage, wie alternative Merkmale auf eine Stichprobe verteilt sind. Derartige Merkmale sind Kopf oder Zahl beim Wurf einer Münze und gut oder schlecht bei der Prüfung von Produkten.
Die Wahrscheinlichkeitsfunktion f(x) für eine Stichprobe n, die klein gegen die Grundgesamtheit ist, mit x Einheiten, die das untersuchte Merkmal tragen, lautet:
![]()
p ist die auf die Grundgesamtheit bezogene Wahrscheinlichkeit, eine Einheit, die das Merkmal trägt, zu finden. Die Grundgesamtheit ist die Menge aller vergleichbaren Einheiten.
Die Wahrscheinlichkeitsfunktion setzt sich zusammen aus der Wahrscheinlichkeit px, x Elemente mit dem Merkmal zu finden, der Wahrscheinlichkeit (1-p)n-x, n-x Elemente zu finden, die das Merkmal nicht tragen und einem Glied, das alle möglichen Reihenfolgen, in denen die Einheiten auftreten können, berücksichtigt, weil diese als gleichwertig angesehen werden. n! (n-Fakultät) ist das Produkt der Zahlen von 1 bis n. Als Definition gilt: 0! = 1. Dies hatten wir bereits oben mit Hilfe des Beispiels zur Kombinatorik plausibel gemacht.
Die Verteilungsfunktion ergibt sich durch Aufsummieren der f(xi).
Beispiel 8, Fortsetzung
| x | f(x) | F(x) |
|---|---|---|
| 0 | 0,32 | 0,32 |
| 1 | 0,42 | 0,74 |
| 2 | 0,21 | 0,95 |
| 3 | 0,046 | 0,996 |
| 4 | 0,004 | 1,000 |
Mit Hilfe der Binomialverteilung berechnen wir für eine Stichprobe n=4 und eine Wahrscheinlichkeit p=0,25 die Wahrscheinlichkeitsfunktion und die Verteilungsfunktion.
Wenn man also vier Teile aus einer Grundgesamtheit mit 25% Fehleranteil prüft, ist die Wahrscheinlichkeit, dass mindestens ein fehlerhaftes Teil in der Stichprobe ist, 68%. Offenbar reicht die Stichprobe selbst bei einem solch hohen Fehleranteil nicht aus, um den Fehler mit einer ausreichenden Wahrscheinlichkeit zu entdecken.
Der Erwartungswert einer Binomialverteilung ist E = np, die Varianz ist σ2 = np(1-p). Die Standardabweichung σ wächst also mit √‾n.Bezogen auf den Erwartungswert nimmt die Standardabweichung jedoch mit der Wurzel aus der Stichprobengröße ab. Dies zeigen die folgenden Abbildungen, in denen Verteilungen mit p=0,25, der Fall von Beispiel 8, und p=0,75 einmal für eine Stichprobe n=4 und dann für eine Stichprobe n=20 aufgetragen sind.
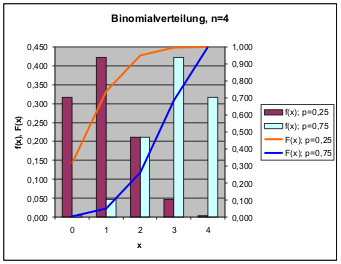
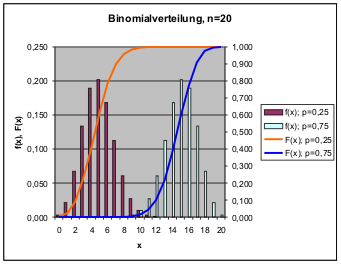
Mit größer werdender Stichprobe stehen um den Schwerpunkt der Verteilung herum mehr Realisierungsmöglichkeiten für die Variable x zur Verfügung. Deshalb konzentrieren sich die Verteilungen mehr um den Erwartungswert und können durch Tests unterschieden werden.
Hypergeometrische Verteilung
Verändern wir die Bedingungen für das Ziehen von Kugeln aus einer Urne so, dass
- nicht zurückgelegt wird und
- die Zahl der entnommenen Kugeln gegenüber der Gesamtzahl der Kugeln nicht vernachlässigbar ist,
hängt die Wahrscheinlichkeit eine schwarze oder eine weiße Kugel zu ziehen vom Ergebnis der vorhergehenden Ziehungen ab. Zur Klärung betrachten wir ein einfaches Beispiel zunächst wieder mit Hilfe eines vereinfachten Baumdiagramms.
Beispiel 9
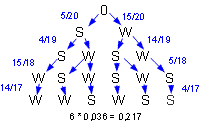 Eine Urne enthält 20 Kugeln. 15 davon sind weiß, 5 schwarz. Wir ziehen 4 Kugeln ohne Zurücklegen und fragen nach der Wahrscheinlichkeit, gerade 2 schwarze Kugeln zu ziehen. Das Baumdiagramm, welches wieder nur die Pfade zeigt, die zum Erfolg führen, lässt erkennen, dass die 6 relevanten Pfade alle die gleiche Gesamtwahrscheinlichkeit haben, obwohl die Wahrscheinlichkeiten für die einzelnen Schritte unterschiedlich sind. Das folgende Ergebnis lässt sich ablesen:
Eine Urne enthält 20 Kugeln. 15 davon sind weiß, 5 schwarz. Wir ziehen 4 Kugeln ohne Zurücklegen und fragen nach der Wahrscheinlichkeit, gerade 2 schwarze Kugeln zu ziehen. Das Baumdiagramm, welches wieder nur die Pfade zeigt, die zum Erfolg führen, lässt erkennen, dass die 6 relevanten Pfade alle die gleiche Gesamtwahrscheinlichkeit haben, obwohl die Wahrscheinlichkeiten für die einzelnen Schritte unterschiedlich sind. Das folgende Ergebnis lässt sich ablesen:
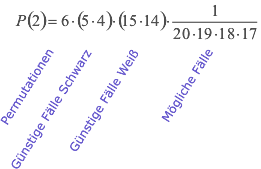
Um das Ergebnis zu verallgemeinern bezeichnen wir mit x die Zahl der gezogenen schwarzen Kugeln, mit k die Größe der Stichprobe, mit s die Zahl der schwarzen Kugeln und mit n die Gesamtzahl der Kugeln und erhalten:
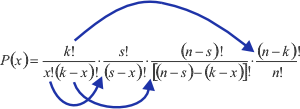
Dabei muss x≤k, k≤s und s≤n sein. Durch Umordnen der Faktoren in der durch die Pfeile angedeuteten Art und mit der abgekürzten Schreibweise
![]()
ergibt sich für die Wahrscheinlichkeit x schwarze Kugeln zu ziehen:
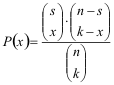
| x | f(x) | F(x) |
|---|---|---|
| 0 | 0,28 | 0,28 |
| 1 | 0,47 | 0,75 |
| 2 | 0,22 | 0,97 |
| 3 | 0,031 | 0,999 |
| 4 | 0,001 | 1,000 |
Hiermit können wir nun die Wahrscheinlichkeiten für die möglichen Ergebnisse des Ziehens von 4 Kugeln aus unserer Urne berechnen.
Verglichen mit dem Ergebnis für die Binomialverteilung ist die Hypergeometrische Verteilung stärker um den Erwartungswert zentriert. Dies ist plausibel, weil extreme Ergebnisse zu Beginn des Ziehens die Chancen bei den restlichen Ziehungen so verschieben, dass ein Ergebnis in der Nähe des Erwartungswertes wahrscheinlicher wird.
Durch Verallgemeinerung des Beispieles erhalten wir also die Wahrscheinlichkeitsfunktion für die hypergeometrische Verteilung:
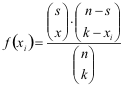
Die Verteilungsfunktion ergibt sich durch Aufsummieren der f(xi). Der Erwartungswert ist, wie bei der Binomialverteilung, E = kp, wenn man p = s/n setzt. Die Varianz ist σ2 = kp(1-p)*(1-k/n). Die Varianz der Binomialverteilung ist hier also durch den Faktor 1-k/n korrigiert, durch den berücksichtigt wird, dass die Breite der Verteilung um so mehr abnimmt, je mehr sich die Stichprobe der Grundgesamtheit annähert. Wenn alle Kugeln aus der Urne entnommen werden, ist schließlich nur noch ein Ergebnis möglich.
Die Hypergeometrische Verteilung beschreibt die Verhältnisse bei der Prüfung einer Stichprobe nach gut und schlecht exakt, während die Binomialverteilung eine Näherung ist, die verwendbar ist, wenn die Grundgesamtheit mindestens 20 mal so groß ist wie die entnommene Stichprobe.
Poisson-Verteilung
Im Gegensatz zur Binomialverteilung und zur Hypergeometrischen Verteilung, bei denen es um die Verteilung von Einheiten geht, die alternative Merkmale tragen, behandelt die Poisson-Verteilung die Zahl der Merkmale pro Einheit. Beispiele hierfür sind die Isolationsfehler pro km Lackdraht, die Beschichtungsfehler pro Schaltschrank, Sicherungsausfälle pro Monat oder die Zahl der Gewinne pro 10 Lose.
Die Wahrscheinlichkeitsfunktion für einen Erwartungswert von λ Merkmalen pro Einheit lautet
![]()
Die Verteilungsfunktion ergibt sich wieder durch Aufsummieren der f(xi).
Beispiel 10
In einem Betrieb wird eine größere Anzahl von Steuerungen eines Herstellers verwendet. Alle Steuerungen haben die gleiche Stromversorgung. Diese ist auf einer Platine untergebracht, die im Mittel über alle vorhandenen Geräte 1,5 Ausfälle pro Monat aufweist. Die Wiederbeschaffungszeit für die Platine beträgt 3 Tage. Der für die Instandhaltung Verantwortliche überlegt sich, wie viele Stromversorgungen er auf Lager halten muss, damit mit 99,5% Wahrscheinlichkeit kein längerer Produktionsausfall durch das Fehlen einer Stromversorgung auftritt.
 Dazu berechnet er den mittleren Fehler in der Wiederbeschaffungszeit.
Dieser beträgt, wenn man den Monat zu 30 Tagen ansetzt, 0,15. Damit werden nun
die Wahrscheinlichkeiten für die Zahl der Ausfälle innerhalb der
Wiederbeschaffungszeit berechnet.
Dazu berechnet er den mittleren Fehler in der Wiederbeschaffungszeit.
Dieser beträgt, wenn man den Monat zu 30 Tagen ansetzt, 0,15. Damit werden nun
die Wahrscheinlichkeiten für die Zahl der Ausfälle innerhalb der
Wiederbeschaffungszeit berechnet.
Um sein Ziel zu erreichen, muss er mindestens 3 Stromversorgungen am Lager haben. Wenn er die erste eingebaut hat, beginnt die Wiederbeschaffungszeit zu laufen. Die Wahrscheinlichkeit dafür, dass innerhalb der nächsten 3 Tage ≤ 2 Ausfälle auftreten ist 99,95%. Dies ist größer als die geplanten 99,5%.
Seine Entscheidung, bei welcher Stückzahl im Lager er nachbestellt, hängt natürlich nicht nur von dieser Berechnung sondern auch von seiner Einschätzung der Risiken bei der Wiederbeschaffung ab.
Kontinuierliche Verteilungen: Die Normalverteilung
Kontinuierliche Verteilungen beziehen sich auf Zufallsvariablen, die innerhalb eines vorgegebenen Bereichs beliebige Werte auf dem Zahlenstrahl annehmen können.
Die Normalverteilung ist eine in der Praxis sehr wichtige Verteilung, weil
die Summe beliebiger kontinuierlicher Zufallsvariablen mit zunehmender Zahl der Summanden immer gegen eine Normalverteilung konvergiert.
 Dieser
zentrale Grenzwertsatz gilt immer, wenn nicht ein Summand in seinem Einfluss überwiegt.
Dieser
zentrale Grenzwertsatz gilt immer, wenn nicht ein Summand in seinem Einfluss überwiegt.
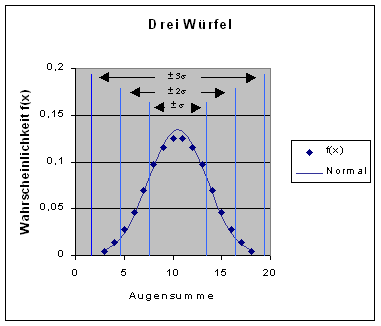
Bei gleichverteilten Zufallsvariablen genügen bereits 3 Summanden, um die Normalverteilung recht gut anzunähern.
Dies zeigt die Abbildung, in der die Wahrscheinlichkeiten der Augensummen beim Würfeln mit 3 Würfeln als Datenpunkte dargestellt sind. Überlagert ist eine Normalverteilung mit dem Mittelwert 10,5 und der Standardabweichung 2,96, die man aus dem Würfelmodell berechnet.
Selbstverständlich ist die Augensumme keine kontinuierliche Zufallsvariable. Die Wahrscheinlichkeitsfunktion wird trotzdem durch die Normalverteilung gut wiedergegeben. Dies zeigt praktisch, daß die Normalverteilung auch auf diskrete Zufallsvariable angewendet werden kann. Da durch die Ungenauigkeit von Meßgeräten oder durch Klassenbildung von Meßwerten immer eine Stufung vorgenommen wird, ist dies eine Voraussetzung für ihre Anwendbarkeit.
Die Wahrscheinlichkeitsfunktion, die bei kontinuierlichen Verteilungen als Wahrscheinlichkeitsdichte bezeichnet wird, ist gegeben durch:
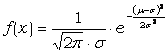
Für die Bildung der Verteilungsfunktion wird, weil die Verteilung kontinuierlich ist, die Summe durch ein Integral ersetzt und man erhält.
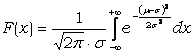
Die Darstellung wird unabhängig vom Mittelwert μ und der Standardabweichung σ, wenn man eine neue Zufallswariable u bildet.
u = (x-µ)/σ
Diese Zufallsvariable hat dann den Erwartungswert 0 und die Varianz (Quadrat der Standardabweichung) 1. Die Normalverteilung für diese Variable (Standardnormalverteilung) ist tabelliert.
Wenn man also die Parameter μ und σ durch Berechnung des Mittelwertes und der Varianz einer Stichprobe geschätzt hat, kann man berechnen, mit welcher Wahrscheinlichkeit bestimmte x auftreten.
Innerhalb der Grenzen ±σ um den Mittelwert liegen 68% der Verteilung, innerhalb ±2σ 95,5% und innerhalb ±3σ 99,73%. Für Fertigungsprozesse müssen daher die Toleranzgrenzen möglichst > 4σ um den Zentralwert liegen, da dann die Ergebnisse des Prozesses zu > 99,99% im zulässigen Bereich erwartet werden können.
Beispiel 11
Ein Zapfen an einem Bauteil wird durch Pressen geformt. Zur Beurteilung des Prozesses wird eine Stichprobe von 50 Teilen in 10 Gruppen zu 5 Teilen entnommen und vermessen. Für den Durchmesser des Zapfens werden die folgenden Werte in mm gemessen:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 24,186 | 24,170 | 24,083 | 24,132 | 24,093 | 24,105 | 24,161 | 24,172 | 24,165 | 24,147 |
| 2 | 24,173 | 24,161 | 24,097 | 24,076 | 24,105 | 24,078 | 24,125 | 24,167 | 24,170 | 24,137 |
| 3 | 24,111 | 24,147 | 24,111 | 24,128 | 24,121 | 24,074 | 24,107 | 24,160 | 24,168 | 24,114 |
| 4 | 24,172 | 24,142 | 24,165 | 24,182 | 24,078 | 24,102 | 24,093 | 24,139 | 24,128 | 24,078 |
| 5 | 24,201 | 24,163 | 24,151 | 24,144 | 24,084 | 24,112 | 24,112 | 24,118 | 24,160 | 24,132 |
Wir untersuchen, ob die Werte normalverteilt sind und welches die aus der Stichprobe geschätzten Parameter der Verteilung sind.
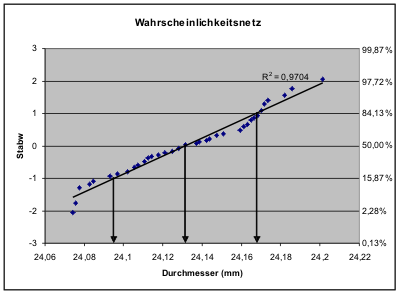
Eine einfache, jedoch subjektive Methode, um auf Normalverteilung zu prüfen, ist die Auftragung der Werte im Wahrscheinlichkeitsnetz. Normalverteilte Werte ergeben hierbei eine Gerade.
Das Wahrscheinlichkeitsnetz ist als Vorlage auf Papier erhältlich oder wird dadurch erzeugt, dass auf der Y-Achse die Variable u der Standardnormalverteilung in einem Bereich von etwa -3 bis +3 linear aufgetragen wird. Den Werten werden die Wahrscheinlichkeiten aus der Verteilungsfunktion der Standardnormalverteilung zugeordnet. Die X-Achse wird so skaliert, dass die Messwerte aufgetragen werden können
Die Grafik wird dadurch erzeugt, dass:
- die Messwerte der Größe nach sortiert werden
- den Messwerten Rangwerte für die Wahrscheinlichkeit zugeordnet werden
- die Rangwerte über den Messwerten aufgetragen werden
Ein erwartungstreuer Wahrscheinlichkeitsrangwert für den i-ten Messwert ist H(i) = i/(n+1), wobei n die Größe der Stichprobe ist.
Die Grafik zeigt, dass die Messwerte recht gut auf einer Geraden liegen. Weil die Anpassung mit Hilfe einer Tabellenkalkulation durchgeführt wurde, das Bestimmtheitsmaß angegeben. Dies sagt aus, dass 97% der Variabilität der Messpunkte durch die Steigung der Ausgleichsgeraden bestimmt werden. Der erste und zweite Messwert liegen deutlich unterhalb der Geraden. Dies deutet darauf hin, dass Durchmesser unterhalb 24,07 mm unterrepräsentiert sein könnten. Ein solcher Effekt kann dadurch zustande kommen, dass der Herstellprozess darauf angelegt ist, kleine Durchmesser zu vermeiden oder dass Teile mit kleinem Durchmesser bereits aussortiert wurden.
Schätzungen für den Mittelwert x‾ und die Standardabweichung s der Stichprobe ergeben sich aus der Auftragung im Wahrscheinlichkeitsnetz aus denn Schnittpunkten der Ausgleichsgerade mit den Werten 0, -1 und +1 auf der Y-Achse. Als Zahlenwerte erhält man:
- x‾= 24,132
- s = (24,168-24,095)/2 = 0,037
Statistiksoftware liefert, wenn auf Normalverteilung geprüft wird, gewöhnlich die Darstellung im Wahrscheinlichkeitsnetz und die Berechnung des Mittelwerts und der Standardabweichung der Stichprobe mit.
Weitere kontinuierliche Verteilungen werden im folgenden Abschnitt besprochen.
Schätzen und Testen
Wenn es darauf ankommt mit Hilfe einer Stichprobe Rückschlüsse auf die Grundgesamtheit zu ziehen oder Stichproben miteinender zu vergleichen, werden statistische Schätz- und Testverfahren angewendet.
Schätzungen
Durch Schätzung werden die Parameter der Verteilung der Grundgesamtheit aus einer Stichprobe ermittelt. Eine Punktschätzung liefert den wahrscheinlichsten Wert für den Parameter, während Bereichsschätzungen den Bereich angeben, in dem der Parameter bei einer vorgegebenen Irrtumswahrscheinlichkeit liegt.
Punktschätzung
In Beispiel 10 haben wir intuitiv den arithmetischen Mittelwert der Ausfälle der Stromversorgungen pro Monat als Schätzwert für den Parameter λ der Poisson-Verteilung verwendet. Da wir beispielsweise auch den Median hätten verwenden können, gilt es zu begründen, dass das arithmetische Mittel der geeignete Schätzer ist. Ein Verfahren dazu ist die Maximum-Likelihood-Methode. Bei dieser Methode wird der Schätzer so variiert, dass die Wahrscheinlichkeit dafür, dass die Stichprobe so auftritt, wie sie gefunden wurde, maximal wird.
Die Verteilungsfunktion selbst wird bei der Anwendung der Maximum-Likelihood-Methode als bekannt vorausgesetzt.
Beispiel 12
Bezeichnen wir den Schätzer für λ mit 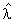 , erhalten wir, wenn wir voraussetzen, dass die Werte poissonverteilt sind, als Wahrscheinlichkeit L dafür, dass in n Monaten gerade x1, x2, x3, ..., xn defekte Stromversorgungen auftraten:
, erhalten wir, wenn wir voraussetzen, dass die Werte poissonverteilt sind, als Wahrscheinlichkeit L dafür, dass in n Monaten gerade x1, x2, x3, ..., xn defekte Stromversorgungen auftraten:
L ist das Produkt der Poisson-Wahrscheinlichkeiten der einzelnen Werte der Stichprobe und wird als Likelihood-Funktion bezeichnet. Da die xi durch die Stichprobe gegeben sind, ist 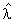 die Größe durch deren Variation ein Maximum von L erreicht werden kann. Das Maximum von L bestimmen wir, indem wir L nach
die Größe durch deren Variation ein Maximum von L erreicht werden kann. Das Maximum von L bestimmen wir, indem wir L nach 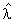 differenzieren und die Ableitung gleich Null setzen. Diese Aufgabe gestaltet sich übersichtlicher, wenn das Produkt durch Logarithmieren der Likelihood-Funktion zunächst in eine Summe umgewandelt wird.
differenzieren und die Ableitung gleich Null setzen. Diese Aufgabe gestaltet sich übersichtlicher, wenn das Produkt durch Logarithmieren der Likelihood-Funktion zunächst in eine Summe umgewandelt wird.
Differenzieren nach 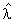 und gleich Null setzen ergibt:
und gleich Null setzen ergibt:
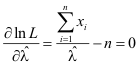
Auflösen nach 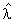 zeigt, dass das arithmetische Mittel in der Tat ein geeigneter Schätzer für den Parameter λ der Poisson-Verteilung ist.
zeigt, dass das arithmetische Mittel in der Tat ein geeigneter Schätzer für den Parameter λ der Poisson-Verteilung ist.
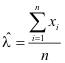
Wenn die Verteilung meherere Parameter hat, die geschätzt werden sollen, gewinnt man durch partielle Ableitung der Likelihood-Funktion nach den Schätzern und gleich Null setzen der Ableitungen die nötige Zahl von Gleichungen, um die Parameter zu bestimmen.
Bereichsschätzung
Wenn man auf der Basis einer Punktschätzung eine Entscheidung trifft, etwa zur Bevorratung von Ersatzteilen, wie das in Beispiel 10 erläutert wurde, besteht neben der Wahrscheinlichkeit, dass die durch die Verteilungsfunktion gegebene Ausfallwahrscheinlichkeit überschritten wird, auch noch das Risiko, dass die tatsächliche mittlere Ausfallwahrscheinlichkeit von dem geschätzten Wert abweicht. Bereichsschätzungen liefern Informationen darüber, wie groß dieses Risiko ist.
Wir gehen also davon aus, dass die aus einer konkreten Stichprobe ermittelte Punktschätzung für den Parameter die Realisierung einer Zufallsvariable ist, die einer Verteilungsfunktion unterliegt. Wenn wir diese Verteilungsfunktion kennen, können wir einen Bereich angeben, in dem der geschätzte Parameter mit einer gegebenen Wahrscheinlichkeit liegt.
Wichtige Parameter und deren Verteilungsfunktionen sind:
| Verteilung Stichprobe | Parameter | Bedingungen | Verteilung Parameter |
|---|---|---|---|
| Normalverteilt | Mittelwert | Standardabweichung der Grundgesamtheit bekannt | Normalverteilt mit der Standardabweichung σ/√n‾ |
| Normalverteilt | Mittelwert | Standardabweichung der Grundgesamtheit aus Standardabweichung der Stichprobe geschätzt | t-verteilt mit der Standardabweichung s/√n‾ und dem Freiheitsgrad n-1 |
| Normalverteilt | Standardabweichung | Standardisiert durch die Teststatistik (n-1)s2/σ2 | Chi-Quadrat verteilt mit dem Freiheitsgrad n-1 |
| Poisson-verteilt | Mittelwert λ | Teststatistik 2nλ. n ist die Zahl der Beobachtungseinheiten | Chi-Quadrat verteilt mit dem Freiheitsgrad 2x für den oberen Grenzwert und 2x+1 für den unteren Grenzwert. x ist die Zahl der Ereignisse in n Beobachtungseinheiten. |
Für die Poisson-Verteilung (Thorndike) und die Binomialverteilung (Larson) sind Diagramme bzw. Nomogramme verfügbar aus denen sich die Vertrauensbereiche für die Schätzung der Parameter der Verteilungen ablesen lassen.
Detaillierter erlätert wird der Weg für die Bereichsschätzung mit zweiseitiger Abgrenzung an dem einfachen Fall des Mittelwertes einer normalverteilten Stichprobe bei bekannter Standardabweichung der Grundgesamtheit.
- Eine Teststatistik wird gebildet, welche den zu schätzenden Parameter mit einer standardisierten Verteilungsfunktion verbindet.
u ist normalverteilt mit dem Mittelwert 0 und der Standardabweichung 1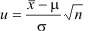
- Die Irrtumswahrscheinlichkeit α für die Bereichsschätzung wird festgelegt.
Wenn uα/2 und u1-α/2 die α/2- und 1-α/2-Quantile der Standardnormalverteilung bezeichnen, liegt die Teststatistik mit der Wahrscheinlichkeit 1-α in dem grün markierten Bereich.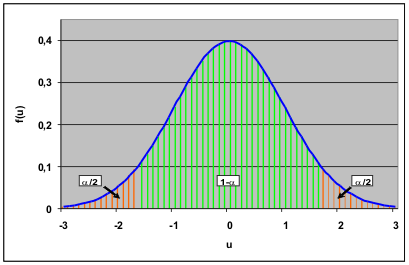
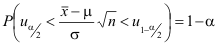
- Der Ausdruck in der Klammer wird den Rechenregeln für Ungleichungen entsprechend so umgeformt, dass die Unter- und Obergrenze von μ durch den Stichprobenmittelwert und die α/2- und 1-α/2-Quantile der Standardnormalverteilung bestimmt werden.
Da uα/2 gleich -u1-α/2 ist, gilt: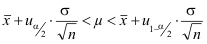
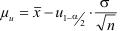
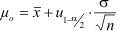
- Der Vertrauensbereich des Mittelwertes ist für eine gegebene Stichprobe und eine gegebene Irrtumswahrscheinlichkeit konstant.
Seine Lage hängt jedoch von der Realisierung der Zufallsvariable x‾ ab.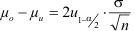
Entsprechend der Irrtumswahrscheinlichkeit α kann der Mittelwert der Grundgesamtheit auch außerhalb des aus der Stichprobe ermittelten Vertrauensbereiches liegen.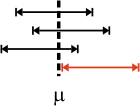
Einseitige Bereichsschätzungen werden analog durchgeführt, indem die Wahrscheinlichkeit 1-α dafür angegeben wird, dass die Teststatistik größer als das α-Quantil der standardisierten Verteilungsfunktion oder kleiner als das 1-α-Quantil der standardisierten Verteilungsfunktion ist.
Die Funktion NORMINV in Microsoft Excel liefert die Quantile der Normalverteilung für eine gegebene kumulierte Wahrscheinlichkeit. Parameter sind der Mittelwert und die Standardabweichung (0;1 bei der Standardnormalverteilung)
Beispiel 13
Der Zapfen, dessen Abmessungen in Beispiel 11 auf Normalverteilung geprüft wurden, soll in eine leicht konische Hüse gefügt werden. Er hat daher das Sollmaß 24+0,2 mm. Untersuchung des Herstellprozesses liefert die Standardabweichung der Grundgesamtheit σ =0,033mm. Um die Einstellung der Maschine zu beurteilen, wird aus der Stichprobe von Beispiel 11 der Mittelwert μ der Grundgesamtheit geschätzt, der mit einer Irrtumswahrscheinlichkeit von 1% nicht unterschritten wird.
μu = x‾- u99%*σ/√n‾= 24,132-2,33*0,033/√5‾0‾= 24,121mm
Der Mittelwert liegt also mit einer Irrtumswahrscheinlichkeit von 1% in der oberen Hälfte des Toleranzbereichs. Der Abstand von der unteren Toleranzgrenze ist mit 3,7 σ hinreichend groß. Problematischer ist es, die obere Toleranzgrenze einzuhalten.
Diese Aussage ist allerdings nicht quantitativ. Um herauszufinden, mit welcher Wahrscheinlichkeit die obere Toleranzgrenze überschritten wird, betrachten wir die Auftragung der Werte im Wahrscheinlichkeitsnetz (Beispiel 11)und lesen 2,3% ab. Da dies offensichtlich zu viel ist, fragen wir, ob denn mit einer zentralen Lage des Prozesses eine akzeptable Ausschussquote zu erreichen ist. Hierzu dividieren wir den Toleranzbereich 0,2mm durch die Standardabweichung der Grundgesamtheit 0,033mm. Bei einer Gesamttoleranz von 6σ ist die gesamte Überschreitungswahrscheinlichkeit 2*G(3), wobei G(u) die Verteilungsfunktion der Standardnormalverteilung ist. Wir erhalten:
P(x<24,0mm) + P(24,2mm<x)=0,24%
Diese Ausfallwahrscheinlichkeit, die einen optimistischen Fall darstellt, ist unter normalen Umständen in einer Serienfertigung nicht zu tolerieren. Es muss daher nach einem Fertigungsverfahren mit einer geringeren Streuung gesucht werden oder die Toleranz muss durch konstruktive Maßnahmen vergrößert werden.
Tests
Statistische Tests dienen generell dem Schluss von einer Stichprobe auf die Grundgesamtheit. Die Schlussweise ist daher induktiv und damit nicht zwingend sondern mit einer Wahrscheinlichkeit < 1 behaftet. Es bedarf also immer einer menschlichen Entscheidung, wie mit dem Ergebnis des Tests verfahren werden soll.
Bei einem statistischen Test wird eine Frage so gestellt, dass sie mit einer vorgegebenen Irrtumswahrscheinlichkeit mit ja oder nein beantwortet werden kann.
Die Fragestellung wird als Hypothese (begründete Vermutung) formuliert. Man unterscheidet zwischen der Nullhypothese H0, die konventionell aussagt, dass die Stichprobe und die Referenz sich nicht unterscheiden und einer Alternativhypothese H1, die einen Unterschied postuliert. Prüft man eine Hypothese mit der Irrtumswahrscheinlichkeit α, können grundsätzlich zwei Arten von Fehlern auftreten:
- Eine zutreffende Nullhypothese wird abgelehnt: Fehler 1. Art, Wahrscheinlichkeit α
- Eine nicht zutreffende Nullhypothese wird nicht abgelehnt: Fehler 2. Art, Wahrscheinlichkeit β
Wir betrachten die grundsätzliche Vorgehensweise bei einem statistischen Test an Hand eines einfachen Beispiels.
Vergleich von zwei Erwartungswerten bei bekannter Varianz
Beispiel 14
- Problemstellung, Nullhypothese, Daten, Irrtumswahrscheinlichkeit und tabellierte Werte
Wir betrachten zwei Stichproben von Stiften aus verschiedenen Fertigungslosen, deren Durchmesser ermittelt wurden. Ziel des Tests ist es festzustellen, ob sich die Mittelwerte der Grundgesamtheiten, aus denen diese Stichproben stammen, signifikant unterscheiden. Unsere Nullhypothese lautet also:
H0: μ1 = μ2
Dies ist eine zweiseitige Fragestellung, weil die Differenz zwischen μ1 und μ2 positiv oder negativ sein kann.
Die Varianzen beider Stichproben setzen wir als bekannt voraus.
Die Eingangsdaten für den Test sind:
Stichprobe 1: n1 = 10 x‾1= 4,161 mm σ1 = 0,012 mm
Stichprobe 2: n2 = 15 x‾2= 4,149 mm σ2 = 0,009 mm
Die Irrtumswahrscheinlichkeit (das Signifikanzniveau) wird auf α = 5% festgelegt. Da die Mittelwerte von Stichproben aus normalverteilten Grundgesamtheiten ebenfalls normalverteilt sind, ist auch die Differenz der Mittelwerte normalverteilt mit der Varianz σd2 und, sofern die Nullhypothese zutrifft, dem Mittelwert 0. Der Grenzwert, gegen den getestet werden muss, ist also:
u1-α/2 = 1,96
- Berechnungen
D = x‾1- x‾2= 0,012 mm
σd2 = (σ12/n1 + σ12/n1)1/2 = 0,004 mm
D/σd = 2,73
- Testanweisung
Die Nullhypothese wird verworfen, wenn gilt:
|D|/σd > u1-α/2
- Testergebnis
2,73 > 1,96 ⇒ H0 wird abgelehnt. Die Stichproben haben mit einer Irrtumswahrscheinlichkeit von 5% nicht den gleichen Mittelwert.
Da die Stichproben aber ein Zufallsergebnis sind, bleibt noch die Frage nach der Reproduzierbarkeit des Ergebnisses oder nach der Wahrscheinlichkeit β eines Fehlers 2. Art.
Berechnung einer Operationscharakteristik
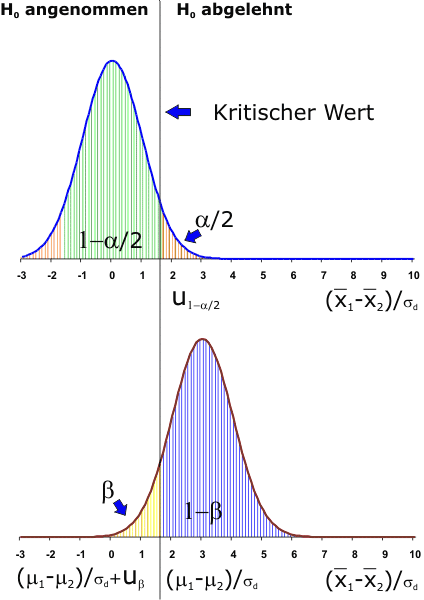
Zunächst sollen die Einflüsse qualitativ mit Hilfe einer Grafik erläutert werden.
Im oberen Teil der Grafik ist die Verteilung der Differenz der Stichprobenmittelwerte entsprechend der Nullhypothese dargestellt. Durch die Irrtumswahrscheinlichkeit ist der kritische Wert festgelegt, bei desssen Überschreitung die Nullhypothese abgelehnt wird.
Wenn sich aber die Mittelwerte der Grundgesamtheiten, die den beiden Stichproben zugrunde liegen, tatsächlich um den Betrag μ1-μ2 unterscheiden, ergibt sich für die Differenz der Stichprobenmittelwerte eine Verteilung, die mit der der Nullhypothese zugeordneten überlappt. Dies ist für den Fall, dass die Differenz der Mittelwerte der Grundgesamtheiten in Einheiten der Standardabweichung dieser Differenz 3 berträgt, im unteren Teil der Grafik dargestellt.
Der Bereich β unterhalb des kritischen Wertes stellt die Wahrscheinlichkeit dar, mit der die Nullhypothese angenommen wird, obwohl sie falsch ist. Diese Wahrscheinlichkeit ergibt sich zunächst nach Festlegung der Irrtumswahrscheinlichkeit durch die tatsächliche Differenz der Mittelwerte der Grundgesamtheiten, die Standardabweichungen und die Größe der Stichproben.
Weil aber gewöhnlich die technische Funktion der Prüflinge eine Begrenzung der Differenz der Mittelwerte der Grundgesamtheiten erfordert, ist festzulegen:
- Die tolerierte Abweichung (nach oben und nach unten bei zweiseitiger Fragestellung)
- Das zugehörige akzeptierte β
Die Operationscharakteristik stellt die Wahrscheinlichkeit des Fehlers 2. Art als Funktion der Differenz der Erwartungswerte der zwei Stichproben dar.
Aufgetragen ist die Wahrscheinlichkeit für das irrtümliche Annehmen der Hypothese gegen die Abweichung der Mittelwerte der Grundgesamtheit in Einheiten der Standardabweichung der Stichprobe mit der Größe der Stichprobe als Parameter. Dabei wurde angenommen, dass n = n1 = n2 und σ = σ1 = σ2 ist. Die Abhängigkeit von der Größe der Stichprobe ergibt sich durch den Zusammenhang zwischen σ und σd.
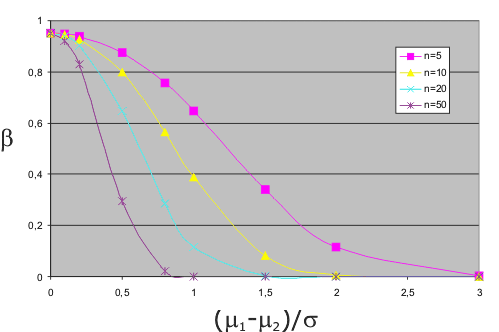
Beispiel 14 (Fortsetzung)
Wir gehen davon aus,
- dass eine Wahrscheinlichkeit von 10% für einen Fehler 2. Art akzeptiert werden kann und
- dass eine technisch relevante Abweichung der Mittelwerte in der Größenordnung der Standardabweichung der Stichprobe liegt,
und fragen nach der erforderlichen Stichprobengröße, um diese zusätzlichen Forderungen zu erfüllen.
Aus der Operationscharakteristik des Tests entnehmen wir, dass bei der ursprünglich verwendeten Gesamtstichprobe von ng = n1 + n2 = 25, was einem n von 12 entspricht, β etwa bei 35% liegt.
Dies ist offensichtlich zu hoch.
Wir legen daher fest, dass β, wenn die Differenz der Mittelwerte gleich σ ist, maximal 10% betragen soll, und entnehmen aus der Operationscharakteristik die die erforderliche Stichprobengröße n = 20. Diese kann erreicht werden, indem aus beiden Losen weitere Teile gemessen werden.
Wichtig sind Vorüberlegungen zum akzeptablen Fehler 2. Art und den daraus resultierenden Anforderungen an die Stichprobengröße
Tests für Erwartungswerte und Varianzen sind in DIN 55 303, Teil 2, genormt. Hier finden sich auch Operationscharakteristiken für die verschiedenen Tests. Statistiksoftware unterstützt die Tests ebenfalls. Bei Unsicherheit über den anzuwendenden Test und die Interpretation der Ergebnisse sollte, sofern Hilfe und Handbücher der verwendeten Software keine ausreichende Information liefern, auf die Fachliteratur zurückgegriffen werden.
Einfluss auf eine Zielgröße
Unter Zielgröße verstehen wir hier eine abgeleitete Größe, die von Zufallsvariablen und eingestellten Parametern abhängt. Dabei kann natürlich auch die Einstellung der Parameter einen zufälligen Anteil enthalten. Beispiele sind:
- Die Verteilung des Gewichts der Passagiere in einem vollbesetzten Flugzeug
- Die Zufriedenheit von Kunden mit Bezug auf gekaufte Produkte und Service
- Die Lebensdauer eines Lagers in Abhängigkeit von Materialkenngrößen, der Oberflächenbehandlung und dem eingesetzten Schmierstoff
Die Fragestellungen bei den drei Beispielen sind unterschiedlich. Im ersten Beispiel ist es für den Flugzeugbauer natürlich von Interesse zu wissen, in welchen Grenzen das Gesamtgewicht der Passagiere bei gegebenem Vertrauensbereich und gegebener Gewichtsverteilung der Passagiere liegen wird. Dies entscheidet darüber, wieviel Gepäck pro Passagier erlaubt werden kann und wieviel Zuladung eingeplant werden kann, ohne das zulässige Startgewicht zu überschreiten.
Die statistische Fragestellung ist in diesem Fall die Fehlerfortpflanzung. Wie wirkt sich die Abweichung des Gewichtes der einzelnen Passagiere vom Mittelwert auf die Verteilung des Gesamtgewichts von n Passagieren aus?
Im zweiten Fall geht es um die Auswertung einer Kundenbefragung. Einfluss auf die Zufriedenheit haben möglicherweise die Kundengruppe, die gekaufte Produktvariante, die Art des mit erworbenen Servicepakets und der Kundendienst, der den Service durchführt. Wenn eine ausreichende Zahl von Datensätzen vorliegt, bei denen die Einstellungen dieser Parameter bekannt sind, erlaubt die Varianzanalyse eine Zuordnung der Parametereinstellungen zu der resultierenden Zufriedenheit.
Das dritte Beispiel beschäftigt sich mit einer Produktoptimierung. Sofern die Lebensdauer von Kugellagern, bei denen Einflussgrößen auf verschiedene Werte eingestellt und sinnvoll miteinander kombiniert wurden, an einer ausreichenden Stichprobe gemessen wurden, kann die erwartete Lebensdauer als Funktion der Parameter dargestellt werden. Die statistische Methodik dazu ist die Regression.
Fehlerfortpflanzung
Ein bewährter Ansatz zur Berechnung der Streuung abgeleiteter Größen aus dem Fehler direkt gemessener Größen ist die Gauß′sche Theorie der Fehlerfortpflanzung. Dies ist eine Näherung, die davon ausgeht, dass die Kenngrößen der gemessenen Stichprobe die Grundgesamtheit mit hinreichender Genauigkeit beschreiben und dass die Streuungen klein gegen die Messgrößen sind. Außerdem wird hier angenommen, dass die einzelnen Einflussgrößen stochastisch unabhängig voneinander sind. Sind sie dies nicht, müssen bei der Berechnung Kovarianzen berücksichtigt werden.
Eine Zufallsvariable z sei eine Funktion von a, b, c,… welche ebenfalls Zufallsvariable sind, z = f(a, b, c, ...). Deren Verteilungen seien charakterisiert durch einen Mittelwert und eine Standardabweichung a‾± σa, b‾± σb, c‾± σc.
Die Differenz zwischen einem Einzelwert und dem Mittelwert einer beliebigen Zufallsvariable x - x‾ soll mit dx bezeichnet werden. Für die Abweichung eines z-Wertes von z‾in Abhängigkeit von den Abweichungen von a, b, c, ... ergibt sich dann:
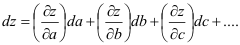
Wenn wir die Varianz einer Stichprobe x1, x2, x3, ..., xn in der Form
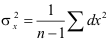
schreiben, erhalten wir, indem wir die dz quadrieren, aufsummieren und mit 1/(n-1) multiplizieren, die Varianz von z als Funktion der Varianzen von a, b, c, ....
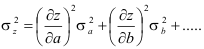
Wir können also σz² aus den experimentell bestimmten Varianzen von a, b, c, ... bestimmen, wenn z eine differenzierbare Funktion dieser Zufallsvariablen ist.
Beispiel 15
Zu den Passagieren einer Fluglinie seien die folgenden an einer Stichprobe aus 51,3% Frauen und 48,7% Männern ermittelten Daten bekannt:
- Gesamtstichprobe: Mittleres Gewicht m‾g(kg): 69,1 Standardabweichung σg(kg): 13,3
- Frauen: Mittleres Gewicht m‾f(kg): 60,6 Standardabweichung σg(kg): 9,6
- Männer: Mittleres Gewicht m‾m(kg): 78,1 Standardabweichung σm(kg): 10,5
- Anteil Männer pro Flug, Mittel a‾m:57% Standardabweichung σa: 8,5%
Wenn wir uns dafür interessieren mit welchem maximalen Gewicht der Passagiere, das wir durch eine Abweichung von +4σ vom Erwartungswert definieren, in einem Flugzeug mit einer gegebenen Zahl von Plätzen gerechnet werden muss, berechnen wir zunächst zur Orientierung einen Erwartungswert. Der ergibt sich, indem wir entsprechend dem Anteil pro Flug die mittleren Gewichte der Männer und Frauen addieren. Für n = 250 Sitze belegt mit 143 Männern und 107 Frauen ergibt das 17653kg. Um die Streuung zu berechnen, können wir verschiedene Wege einschlagen.
Der "Worst Case"
Hier nehmen wir an, dass das Gewicht aller Frauen und Männer 4σ über dem Mittelwert liegt und dass auch der Anteil der Männer an der oberen Grenze liegt. Mit diesen Annahmen erhalten wir ein Gesamtgewicht von
Mmax = 250*(0,91*(78,1+4*10,5)+0,09*(60,6+4*9,6)) = 29550kg
Das ist ein Zuschlag von 67% auf den Erwartungswert. Doch entspricht das wirklich dem Ziel, das Gewicht innerhalb der Grenzen von 4σ zu berechnen? Sicher nicht, denn dadurch, dass 250 Einzelgewichte und der Anteil Männer mit einer Wahrscheinlichkeit von je 3,17*10-5kombiniert werden, hat dieser Fall eine verschwindend geringe Wahrscheinlichkeit. Um eine Auslegung auf unnötig hohe Gewichte zu vermeiden, müssen wir die Streuung des Gesamtgewichts mit Hilfe der Fehlerfortpflanzung berechnen.
Berechnung für gegebenes a
Wir setzen a auf die 4σ-Grenze 91% Männer und berechnen für diesen Fall die Standardabweichung des Gesamtgewichts. Ziehen wir dafür die Daten der Gesamtstichprobe heran, erhalten wir:
Mtot = mg1+mg2+mg3+ .... +mg250
Damit wird
dMtot = dmg1+dmg2+dmg3+ .... +dmg250
und
σtot² = σg1²+σg2²+σg3²+ ... σg250² = 250*σgi,
da die σgi alle gleich sind. Die Zahlenrechnung ergibt für diesen Fall σtot = 210kg. Mit einem mittleren Gewicht bei 91% Männern von 19131kg ergibt sich ein Maximalgewicht von
Mmax = 19131kg + 4*210kg = 19971kg
Dieser Wert überschreitet den Erwartungswert nur noch um 13%, obwohl das Maximalgewicht immer noch überschätzt wird. Eine erste Korrektur erreichen wir, indem wir zur Berechnung von σtot die Daten aus den Gewichtsverteilungen von Männern und Frauen heranziehen. Dazu schreiben wir:
Mtot = Mm + Mf
Dann ist:
σtot² = σMm²+σMf²
σMm² und σMf² berechnen wir aus den Standardabweichungen der Gewichte von Männern und Frauen zu:
σMm = (250*0,91)1/2*σm = 158,4kg σMf = (250*0,09)1/2*σm = 45,5kg
Daraus resultiert ein σtot von 164,8kg und damit ein Mmax von 19790kg. Die Verwendung der differenzierten Kenntnisse über die Gewichtsverteilung von Männern und Frauen führen zu einer weiteren Reduzierung der erforderlichen Toleranz.
Berücksichtigung der Streuung von a
Weil Mtot keine explizite Funktion von a, dem Anteil der Männer an den Passagieren eines Flugs, ist, kann die Methode der Fehlerfortpflanzung nicht ohne weiteres auf unser Problem angewendet werden. Als Näherung setzen wir:
Mtot = M′m + M′f + M′a
Um die Variablen zu trennen werden M′m und M′f als Gesamtgewichte der Männer bzw. Frauen bei mittlerem a definiert. M′a ist dann der Gewichtsanteil, der durch den Austausch von Männern und Frauen zur Anpassung an das tatsächliche a entsteht. Die gesamte Varianz von Mtot ist dann:
σtot² = σMm²+σMf²+σMa²
σMm² und σMf² berechnen wir wie im vorigen Abschnitt:
σMm = (250*0,57)1/2*σm = 125,3kg σMf = (250*0,43)1/2*σm = 99,5kg
Damit M′a nur von a abhängt und problemlos differenziert werden kann, berücksichtigen wir für den Austausch von Männern und Frauen nur die mittleren Gewichte der beiden Geschlechter und setzen:
M′a = n*a*(m‾m- m‾f)
Damit ergibt sich:
dM′a = n*(m‾m- m‾f)da
und daraus
σMa² = n²*(m‾m- m‾f)²*σa² σMa = 250*(78,1 - 60,6)*0,085 = 371,9kg
Mit diesen Anteilen ergibt sich für die gesamte Streuung des Gewichtes σtot = 404,9kg. Da wir nun bei der Berechnung des Maximalgewichtes innerhalb der 4σ-Grenze von dem mittleren Gewicht der Passagiere ausgehen, erhalten wir:
Mmax = 17653kg + 4*405kg = 19273kg
Insgesamt ergibt sich so ein Zuschlag von 9,2% auf das mittlere Gewicht. Mit dieser Rechnung haben wir allerdings die Streuung etwas unterschätzt, weil wir die Varianz, die durch die Abweichung der ausgetauschten Männer und Frauen vom mittleren Gewicht entsteht, vernachlässigt haben.
Insgesamt zeigt das Beispiel, dass durch die statistische Toleranzrechnung mit Hilfe der Gauß′schen Fehlerfortpflanzung bei
- einer langen "Maßkette" (n=250),
- Toleranzen der einzelnen Maße von ca. 15% und
- einer beachtlichen Toleranz hinsichtlich der Elemente, aus denen sich die "Maßkette" zusammensetzt,
eine praktikable Einengung der Gesamttoleranz erreicht werden kann. Auf wie viele Standardabweichungen man die Toleranz auslegt, hängt natürlich von dem Risiko ab, das mit einer Überschreitung der Toleranz verbunden ist.
Varianzanalyse
Auf dieser Seite
Entsteht eine kurze Einführung zu den statistischen Grundlagen von Zuverlässigkeit, Versuchsplanung und der Auswertung von Lebensdauerdaten

 QM-SYSTEME
QM-SYSTEME