NEU

Wichtige Änderungen:
• Seite überarbeitet
• Die Inhalte der Seite http://www.smqe.de/smqe/doe /design.htm wurden übernommen

---

Letzte Änderung:
07 May 2008

•  HOME
•  QM-SYSTEME
  •  Grundlagen
  •  Die ISO 9000-Familie
  •  ISO/TS 16949:2002
    •  TS 16949 Aufbau
    •  TS 16949 Forderungen
  •  Aufbau
    •  Vorgehen
    •  Aufwand
    •  Prozesse
    •  Dokumentation
•  QM-METHODEN
  •  Übersicht
  •  QFD
  •  FMEA
    •  Grundlagen
    •  Kurzanleitung
    •  Beispiel
  •  Statistik
    •  Einführung
    •  Zuverlässigkeit
    •  Versuche
    •  Weibull Statistik
  •  Problemlösung
•  KONTAKT
  •  Über SMQE
  •  Kontakt
  •  Impressum
  •  Sitemap
•  DOWNLOAD
  •  Formulare, Anleitungen

QM-Methoden » Statistik » Versuche

Druckversion

Versuchsplanung: Mehrfaktorenexperimente

Die Qualität eines Produktes, einer Dienstleistung oder eines Prozesses hängt gewöhnlich von einer Vielzahl von Einflussfaktoren ab, die untereinander wechselwirken können. Einflussfaktoren sind Größen, die als Eingaben in das System oder als Steuerparameter spezifiziert sind. Aber auch die Umgebungsbedingungen und die Menschen, die Prozesse durchführen, die Produkte herstellen und nutzen und Dienstleistungen erbringen, beeinflussen die Qualität eines Systems.

Aus der Funktionsanalyse und der FMEA sind die für die Funktion des Gesamtsystems kritischen Komponenten bekannt.

Versuchsplanung muss nun zum Ziel haben, die erforderlichen Daten

• mit hoher statistischer Signifikanz,
• in kurzer Zeit und
• mit einer geringen Anzahl von Versuchen

zu ermitteln.

Das klassische Verfahren, einen Parameter zu variieren, alle anderen konstant zu halten und dann den nächsten zu variieren, liefert zwar die volle gewünschte Information, führt aber bei einer größeren Anzahl von Parametern schnell zu einem ausufernden Aufwand. Es gilt daher, durch einen bewussten Verzicht auf Information den Aufwand zu begrenzen.

Ein erprobter Weg dahin ist der faktorielle Versuch.

Mathematisches Modell

Möchte man k Einflussgrößen (Parameter) auf jeweils n Einstellungen untersuchen, ergibt das eine Gesamtzahl von

(1)

Versuchen. Eine minimale Information über den Zusammenhang zwischen einer Zielgröße y und einem Parameter x_j ergibt sich, wenn man den Parameter auf n = 2 Stufen variiert. Weil dann von der Funktion y = f(x_j) nur zwei Wertepaare bekannt sind, wird implizit ein linearer Zusammenhang angenommen. Für die Bestimmung des Funktionswertes am Koordinatenursprung und von k Steigungen für die Einflüsse der einzelnen Parameter sind aber nur k + 1 Versuche erforderlich. Ein faktorieller Versuch auf 2 Stufen kann also noch weitere Informationen liefern.

Um diese Information festzulegen, nehmen wir an, dass der Zusammenhang zwischen der Zielgröße und den Parametern durch ein Polynom gegeben ist, in dem neben Potenzen der einzelnen Parameter auch gemischte Glieder vorkommen, in denen die Parameter mit beliebigen Potenzen vertreten sind. Da wir uns aber auf 2 Stufen beschränkt haben, berücksichtigen wir nur Glieder, in denen die einzelnen Parameter linear auftreten. Für 3 Parameter ergibt sich:

(2)

Damit erhalten wir gerade 2^k Koeffizienten, die durch den Versuchsplan bestimmt werden können.

Zur Vereinfachung der Lösung des inhomogenen linearen Gleichungssystems, das resultiert, wenn wir aus den 2^k Versuchsergebnissen und den in den einzelnen Versuchen eingestellten Werten für die Parameter die Koeffizienten berechnen wollen, nehmen wir eine Koordinatentransformation vor. Wir definieren:

(3)

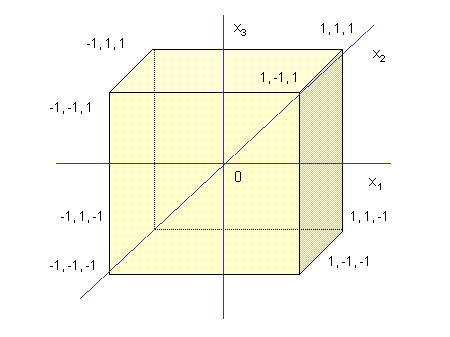
(1) und (2) bezeichnen die beiden Einstellungen des Parameters x_j. In den neuen Koordinaten liegt nun der Ursprung im Zentrum des Versuchs und die beiden Einstellungen sind jeweils -1 und +1(Abb. 1).

Abb. 1	Faktorieller Versuchsplan mit 3 Parametern im transformierten Koordinatensystem

Damit nimmt das lineare Gleichungssystem die folgende Form an:

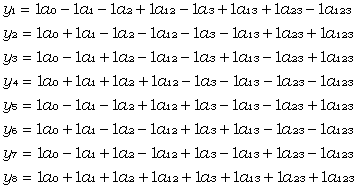
(4)

Es ist nun offensichtlich, dass die a_i durch zweckmäßige Addition und Subtraktion der Gleichungen (4) recht einfach ermittelt werden können.

Man erhält:

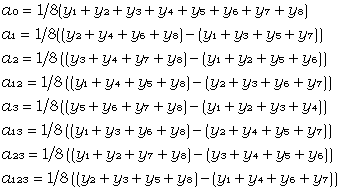
(5)

In der Literatur wird meistens A₁ = 2a₁ als Effekt des Parameters 1 bezeichnet. Dies ist dann die Auswirkung der Einstellung des Parameters auf den Stufen +1 und -1.

Mathematisch gesehen ist die Koeffizientenmatrix des Gleichungssystems (4) orthogonal. Orthogonale Matrizen vermitteln längentreue Abbildungen und ihre Determinanten können nur die Werte +1 und -1 annehmen. Dies bedeutet, dass faktorielle Versuchspläne, die nach dem beschriebenen Muster konstruiert sind, immer zu einem lösbaren Gleichungssystem führen. Außerdem sind die Versuche so im Parameterraum angeordnet, dass Effekte und Wechselwirkungen aus den Versuchsergebnissen ohne Verzerrungen ermittelt werden können. Orthogonal im streng mathematischen Sinne können nur quadratische Matrizen sein. In der Literatur werden auch Versuchspläne, die für die einzelnen Spaltenvektoren die Bedingungen Σx_ix_j = 0 und Σx_i= 0 erfüllen, als orthogonal bezeichnet. Generell ist die Erfüllung dieser Bedingungen hinreichend für einen ausgewogenen Versuchsplan mit linear unabhängigen Effekten.

Weil Mehrfachwechselwirkungen erfahrungsgemäß klein sind, ergibt sich die Möglichkeit den Vektor der Koeffizienten für die dreifache Wechselwirkung in (6) mit einem vierten Parameter zu belegen. Damit ergibt sich ein reduzierter faktorieller Versuch. In unserem Beispiel, das in (6) als Koeffizientenmatrix dargestellt ist, können wir so mit 8 Versuchen die Einflüsse von 4 Parametern untersuchen.

Nr.	Versuchsplan				Koeffizientenmatrix								(6)
	x1	x2	x3	x4	a0	a1 a234	a2 a134	a12 a34	a3 a124	a13 a24	a23 a14	a123 a4
1	-1	-1	-1	-1	+	-	-	+	-	+	+	-
2	+1	-1	-1	+1	+	+	-	-	-	-	+	+
3	-1	+1	-1	+1	+	-	+	-	-	+	-	+
4	+1	+1	-1	-1	+	+	+	+	-	-	-	-
5	-1	-1	+1	+1	+	-	-	+	+	-	-	+
6	+1	-1	+1	-1	+	+	-	-	+	+	-	-
7	-1	+1	+1	-1	+	-	+	-	+	-	+	-
8	+1	+1	+1	+1	+	+	+	+	+	+	+	+

Dies wird allerdings mit einem weiteren Verlust an Information erkauft, denn die Wechselwirkungen der Parameter sind nun miteinander vermischt. Die Koeffizientenmatrix (6) zeigt, dass bei einer Lösung des Gleichungssystems nach (5) die Effekte der Parameter nicht von den komplementären dreifachen Wechselwirkungen getrennt werden können. Ebenso sind alle Zweifachwechselwirkungen untrennbar mit ihren Komplementen verbunden. Die sinnvolle Anwendung von teilfaktoriellen Plänen setzt also vernachlässigbare Wechselwirkungen voraus.

Daraus folgt, dass für eine erfolgreiche Versuchsplanung eine gute Kenntnis des zu untersuchenden Systems mit der erforderlichen Methodenkenntnis vereint werden muss. Als Faustregel gilt aber, dass Wechselwirkungen zwischen Parametern in chemischen Systemen erheblich wahrscheinlicher sind als in mechanischen. Auf der Ebene der chemischen Elementarschritte ist hierfür der exponentielle Einfluss der Temperatur und die multiplikative Verknüpfung des Exponentialglieds mit der Konzentration der beteiligten Stoffe verantwortlich. Das Versagen mechanischer Systeme wird dagegen eher durch mechanische Spannungen bestimmt, die sich additiv aus den Beiträgen verschiedener Parameter zusammensetzen.

Zur Optimierung von Produkten und Prozessen durch statistische Versuchsplanung muß zwar die Zielgröße auf einer Skala, die die Unterscheidung von besser oder schlechter erlaubt, also mindestens auf einer Ordinalskala, messbar sein. Als Faktoren können jedoch auch Größen verwendet werden, die lediglich nach gleich oder ungleich, also auf einer Nominalskala, unterschieden werden. Dadurch ist die statistische Versuchsplanung auch zur Optimierung von administrativen Prozessen geeignet.

Nach oben ⇑

Ein Beispiel

Ein Unternehmen verliert Aufträge, weil die Durchlaufzeit für Angebote zu hoch ist. In einem Projekt zur Lösung dieses Problems wurden drei möglicherweise relevante Ursachenkomplexe identifiziert:

Zu den drei Ursachenkomplexen werden Lösungsvorschläge erarbeitet. Um deren Wirksamkeit und Praktikabilität zu erproben, wird ein Pilotprojekt gestartet, in dem Angebote ganz oder teilweise nach dem neuen Verfahren ausgearbeitet werden. Das Pilotprojekt wird nach einem einfachen statistischen Versuchsplan durchgeführt. Faktoren und Einstellungen sind:

Da Wechselwirkungen nicht auszuschließen sind, werden 8 Versuche geplant. Jeder Versuch wird dreimal durchgeführt und die Reihenfolge der Versuche wird zufällig gewählt. Damit werden Störeinflüsse eliminiert und genügend Material für eine statistische Auswertung gesammelt. Für das Projekt wird der folgende Versuchsplan erstellt, bei dem in der Spalte Durchlaufzeit die Ergebnisse der Versuche eingetragen sind

Versuchsnr.	Lfd. Nr	Schnittstellen	Parallelarb.	Lieferanten	Durchlaufzeit
6	1	1	-1	1	5,9
9	2	-1	-1	-1	4,8
20	3	1	1	-1	9,5
23	4	-1	1	1	8,5
18	5	1	-1	-1	6,7
1	6	-1	-1	-1	4
7	7	-1	1	1	8,5
5	8	-1	-1	1	4,8
2	9	1	-1	-1	6
3	10	-1	1	-1	8,1
15	11	-1	1	1	8,3
22	12	1	-1	1	7,1
14	13	1	-1	1	6,3
13	14	-1	-1	1	5,7
11	15	-1	1	-1	7,1
10	16	1	-1	-1	5,8
24	17	1	1	1	9,5
16	18	1	1	1	11
8	19	1	1	1	10
19	20	-1	1	-1	8,2
17	21	-1	-1	-1	5
12	22	1	1	-1	8,8
21	23	-1	-1	1	4,9
4	24	1	1	-1	9,8

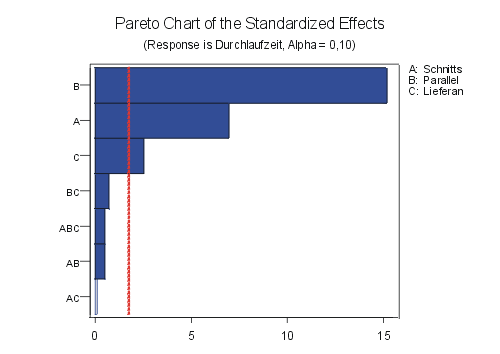
Die Berechnung der Effekte mit Hilfe der Statistiksoftware Minitab bringt folgendes Ergebnis:

Abb. 2	Durchlaufzeit Angebote: Effekte und Wechselwirkungen

Die Effekte werden in standardisierter Form, als Vielfache der Standardabweichung dargestellt. Ergebnis ist hier die Durchlaufzeit. Die gestrichelte Linie gibt das Niveau an, bis zu dem die Effekte und Wechselwirkungen bis zu einem Vertrauensbereich von 90% (alpha=0,1) signifikant sind.

Detailliertere Ergebnisse liefern die tabellarische Darstellung der Berechnung der Effekte und Wechselwirkungen aus einer Regressionsanalyse und die Varianzanalyse.

Estimated Effects and Coefficients for Ergebnis (coded units)
Term	Effect	Coef	SE Coef	T	P
Constant		7,26250	0,1106	65,65	0,000
Schnitts	1,54167	0,77083	0,1106	6,97	0,000
Parallel	3,35833	1,67917	0,1106	15,18	0,000
Lieferan	0,55833	0,27917	0,1106	2,52	0,023
Schnitts*Parallel	0,10833	0,05417	0,1106	0,49	0,631
Schnitts*Lieferan	-0,02500	-0,01250	0,1106	-0,11	0,911
Parallel*Lieferan	0,15833	0,07917	0,1106	0,72	0,485
Schnitts*Parallel*Lieferan	0,10833	0,05417	0,1106	0,49	0,631

In der Tabelle bedeuten:

Term:	Faktor, Wechselwirkung
Effect:	Größe des Effektes oder der Wechselwirkung
Coef:	Koeffizienten des Effektes oder der Wechselwirkung im Regressionspolynom. Da im Beispiel alle Faktoren auf einer Nominalskala eingestellt wurden, ist das Regressionspolynom, welches prinzipiell die Berechnung der Zielgröße für beliebige Einstellungen der Faktoren innerhalb des durch den Versuch umschlossenen (Hyper-)Raumes ermöglicht, ohne Bedeutung.
SE-Coef:	Standardabweichung der Koeffizienten. Da alle Faktoren auf der gleichen Nominalskala skaliert sind, sind die Standardabweichungen gleich.
T:	Quotient aus Koeffizient und Standardabweichung, Vergleich mit der entsprechenden Schranke der T-Verteilung liefert eine Aussage über die Signifikanz des Effektes oder der Wechselwirkung.
P:	Die Wahrscheinlichkeit dafür, daß es falsch ist, die Hypothese der Effekt sei signifikant, anzunehmen.

Das Modell für die Varianzanalyse ist eine zeifache Kreuzklassifikation mit mehreren Beobachtungen pro Faktorenkombination. Dieses Modell liefert auch bei Wechselwirkungen der Faktoren untereinander Werte, aus denen die zufällige Versuchsstreuung ermittelt werden kann. Die dreifache Wiederholung des Versuchsplans führt zu einem relativ kleinen Anteil der Varianz, der auf die zufällige Streuung der Durchlaufzeiten zurückzuführen ist.

Analysis of Variance for Ergebnis (coded units)
Source	DF	SS	MS	F	P
Main Effects	3	83,8013	27,9338	95,09	0,000
2-Way Interactions	3	0,2246	0,0749	0,25	0,857
3-Way Interactions	1	0,0704	0,0704	0,24	0,631
Residual Error	16	4,7000	0,2937
Total	23	88,7963

Die Größen haben die folgenden Bedeutungen:

Source:	Quelle der Variabilität des Ergebnisses
DF:	Degree of Freedom, Freiheitsgrad. Wenn n Werte gemessen werden und der Mittelwert bekannt ist, lassen sich n-1 Meßwerte frei variieren. n-1 wird dann als Freiheitgrad bezeichnet. Da bei der Varianzanalyse die gesamte Varianz der Meßwerte in Anteile der einzelnen Quellen aufgepalten wird, wird auch der gesamte Freiheitsgrad des Versuchsplans anteilig den einzelnen Quellen zugeordnet.
SS:	Sum of Squares, Summe der Abweichungsquadrate, die auf diese Quelle zurückzuführen ist.
MS:	Mean Sum of Squares, SS dividiert durch DF. MS ist der der Quelle zuzuordnende Anteil der Varianz
F:	Quotient aus MS für den Effekt oder die Wechselwirkung und MS für den Restfehler, Vergleich mit der entsprechenden Schranke der F-Verteilung liefert eine Aussage über die Signifikanz des Effektes oder der Wechselwirkung.
P:	Die Wahrscheinlichkeit dafür, daß es falsch ist, die Hypothese der Effekt sei signifikant, anzunehmen.

Die Analyse zeigt, daß die SS für den Restfehler ziemlich klein ist. Daher hätten auch zwei Wiederholungen des Versuchs ausgereicht, um die Signifikanz der Haupteffekte nachzuweisen. Um dies im Vorfeld abschätzen zu können, sind Kenntnisse über die Versuchsstreuung von Nutzen.

Insgesamt bestätigt der Versuch, daß die Reduzierung der Schnittstellen und besonders die parallele Abwicklung von Planung und Anfrage bei Unterlieferanten Maßnahmen sind, die dauerhaft eingeführt werden sollten.

Da bei diesem Versuch die Einstellung der Faktoren zu einem guten Teil auf menschlichem Verhalten beruht, welches bereits durch die Aufmerksamkeit, die es durch die Durchführung des Versuchs erhält, beeinflußt werden kann, zeigt das Versuchsergebnis eher ein Potential, zu dessen Ausschöpfung neben einer Umstellung der Vorgehensweise auch Schulung und persönliche Motivation erforderlich ist.

Nach oben ⇑

Optimierung

Versuche in der beschriebenen Form liefern mit relativ geringem Aufwand eine Antwortfunktion, die in dem durch die Parametereinstellungen aufgespannten Hyperraum gültig ist.

(7)

Die b sind dabei die Koeffizienten des durch die Auswertung der Versuche ermittelten Regressionspolynoms. Obwohl die Antwortfläche wegen auftretender Wechselwirkungen "verdreht" sein kann, treten keine Minima oder Maxima auf. Das bedeutet, dass das Ergebnis des Versuchplans Auskunft über bessere oder schlechtere Parametereinstellungen (und auch über das Erreichen von Zielwerten) gibt, aber keine Auskunft darüber, ob ein Optimum erreicht ist.

Zum raschen Auffinden eines Optimums existieren mehrere Methoden, die in ihren Grundgedanken weitgehend übereinstimmen, sich aber in den Details der Vorgehensweise unterscheiden. Kurz erläutern wollen wir hier die Methode des steilsten Anstiegs, die grundsätzlich sehr anschaulich ist, aber nicht optimal für den Rechnereinsatz.

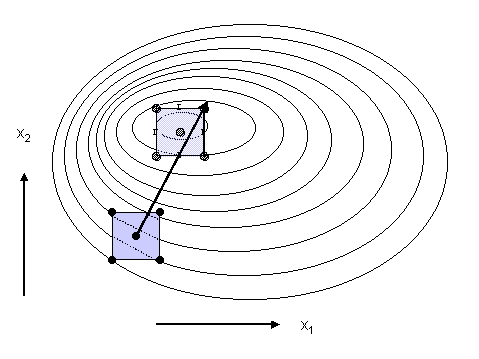
Der Einfachheit halber betrachten wir ein System mit 2 Parametern ohne nennenswerte Wechselwirkungen. Das Ergebnis eines faktoriellen Versuches, hier mit einem zusätzlichen Versuch am Zentralpunkt, lässt sich als Projektion der Funktion y(x₁, x₂) in Form von Höhenlinien auf die x₁, x₂-Ebene darstellen (Abb. 3). Sofern Wechselwirkungen tatsächlich vernachlässigt werden können, nähert das aus dem Versuchsergebnis berechnete Regressionspolynom den Verlauf der Höhenlinien innerhalb der durch den Versuch abgedeckten Fläche durch parallele Geraden mit gleichem Abstand an.

Abb. 3	Methode des steilsten Anstiegs

Die Richtung des steilsten Anstiegs ist die Senkrechte auf den Höhenlinien mit dem Fußpunkt im Zentrum des Versuchs. Auf dieser Linie werden nun weitere Versuche geplant, indem man die Schrittweite für den Parameter, der den größten Effekt hat, festlegt. Die Schrittweite(n) für den (die) anderen Parameter wird (werden) so angepasst, dass die Versuche auf der Linie des steilsten Anstiegs liegen. In der in Abb. 3 dargestellten Situation würde sich für den Parameter mit dem größten Effekt, x₂, die Schrittweite 1 anbieten. x₁ kann aus der Beziehung

(8)

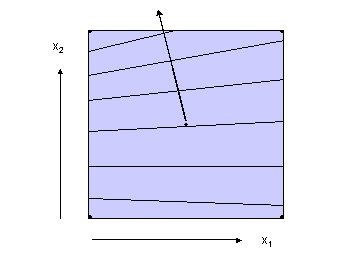
ermittelt werden. Wenn Wechselwirkungen nicht zu vernachlässigen sind, hängt die Richtung des steilsten Anstiegs vom Ort ab und wird zweckmäßig an der Grenze des untersuchten Gebiets festgelegt (Abb. 4).

Abb. 4	Steilster Anstieg bei Wechselwirkungen

Ist diese Planung durchgeführt, werden in einem nach Kenntnis des Systems vernünftig erscheinenden Abstand vom untersuchten Bereich einzelne Versuche durchgeführt, um festzustellen, wie sich das System verhält. Die Auftragung der Versuchsergebnisse entlang der Linie des steilsten Anstiegs ergibt einen Trend, aus dem abgeschätzt werden kann, bei welchem Schritt ein Optimum oder der angestrebte Zielwert zu erwarten ist. Hier wird ein Bestätigungsversuch durchgeführt.

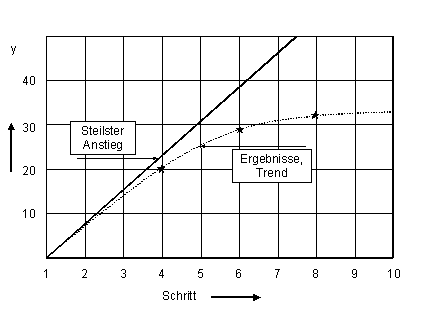
Abb. 5	Auftragung der Zielgröße entlang der Linie des steilsten Anstiegs

In dem Beispiel nach Abb. 5 wurden für den 4., den 6. Und den 8. Schritt Versuche durchgeführt. Das Ergebnis des 8. Schrittes zeigt, dass auf der Linie des steilsten Anstiegs ein Optimum bzw. Plateau erreicht ist oder bald erreicht sein wird. Daher sollte die Untersuchung mit dem 10. Schritt fortgesetzt werden. Wenn sich hier ein Abfall des Zielwertes zeigt, wird ein weiterer faktorieller Versuch mit den Einstellungen des 10. Schrittes als Eckpunkt gestartet (Schritt 10 ist bereits der erste Versuch des neuen Versuchsplans, Abb. 2). Durch den Versuch am Zentralpunkt können Hinweise gewonnen werden, ob das Parameterfeld ein Extremum einschließt. Sofern diese Hinweise stark sind, kann der Plan durch Hinzufügen von Versuchspunkten auf den Seitenmitten zu einem Plan auf 3 Levels ausgebaut werden, der auch die Berechnung quadratischer Effekte gestattet. Damit kann dann ein Extremwert innerhalb der durch den Versuchsplan abgedeckten Parametereinstellungen bestimmt werden. Ist kein Extremwert vorhanden, sollte der steilste Anstieg neu bestimmt und die Prozedur in der neuen Richtung fortgesetzt werden.

Statistische Versuchsplanung, zu der immer auch eine Versuchsauswertung mit Hilfe statistischer Verfahren gehört, eignet sich zur wirtschaftlichen Gewinnung von Daten zur Zuverlässigkeit. Sie sollte nicht nur für die Optimierung von Produkten und Prozessen, sondern auch zum Design von Schnelltests verwendet werden.

Gängige Statistiksoftware enthält Module zur statistischen Versuchsplanung, die den Anwender beim Entwurf von Versuchsplänen und bei der Auswertung der Versuche wirksam unterstützen. Kenntnis der Grundlagen ist trotzdem unerlässlich, weil die Gewinnung von zuverlässigen Daten bei minimalem experimentellem Aufwand nur dann möglich ist, wenn der Anwender in der Lage ist, aus seiner Systemkennntnis heraus bewusste Entscheidungen zur Versuchsplanung zu treffen.