|
QM-Methoden » Statistik » Zuverlässigkeit |
Druckversion |
Zuverlässigkeit und Wartungsfreundlichkeit
Zuverlässigkeit und Wartungsfreundlichkeit sind wichtige Qualitätsmerkmale eines Produktes. Sie werden in erster Linie durch die Konstruktion festgelegt. Aber auch die Herstellung, die Art, wie der Nutzer das Produkt gebraucht, und die Wartung sind von erheblichem Einfluss.
Das Sicherstellen von Zuverlässigkeit und Wartungsfreundlichkeit ist also ein wesentliches Ziel einer Reihe von Geschäftsprozessen des Herstellers:
- Im Angebotsprozess werden die Forderungen des Kunden an die Zuverlässigkeit und Wartungsfreundlichkeit des Produktes erfragt, geklärt und in ein Konzept umgesetzt.
- Im Planungs- und Entwicklungsprozess wird das Konzept ausgearbeitet. Die Erfüllung der Forderungen wird verifiziert.
- Im Beschaffungsprozess werden Fremdleistungen so eingebunden, dass die gewünschte Zuverlässigkeit und Wartungsfreundlichkeit resultiert.
- Im Herstellprozess wird sichergestellt, daß die Zuverlässigkeit des Produktes nicht durch vorzeitige Ausfälle beeinträchtigt wird.
- Durch den Serviceprozess werden die geplante Zuverlässigkeit und Wartungsfreundlichkeit realisiert. Verbesserungspotentiale werden erkannt und, soweit sie sich in der Nutzungsphase des Produktes ausschöpfen lassen, genutzt. Sonst fließen sie in Änderungen oder Neuentwicklungen ein.
Die Ziele von Geschäftsprozessen werden erreicht,
- wenn die Prozesse geplant werden,
- wenn die Ergebnisse auf Übereinstimmung mit den geplanten Zielen geprüft werden und
- wenn die Ursachen von Abweichungen durch einen ständigen Verbesserungsprozess eliminiert werden.
Daher sind Zuverlässigkeit und Wartungsfreundlichkeit einerseits als Teil des Qualitätsmanagements eine Managementaufgabe. Andererseits sind die Kennzahlen, die Zuverlässigkeit und Wartungsfreundlichkeit beschreiben, Zufallsvariable. Daher ist sowohl für die Berechnung dieser Kennzahlen als auch für die Planung der Zuverlässigkeit und Wartungsfreundlichkeit eines Produktes eine statistische Modellbildung erforderlich. Diese kann sehr komplex sein und erfordert daher gewöhnlich die weitestgehende Vereinfachung, die ohne Verlust der Aussagekraft möglich ist.
Grundsätzliche Konzepte werden am Beispiel einer Produktionsanlage erläutert.
Kundennutzen
Ein Kunde, der in eine Produktionsanlage investiert, möchte damit einen Beitrag zur Existenzsicherung seines Unternehmens leisten. Dies wird gelingen, wenn die Anlage
- die geforderte Funktion qualitativ einwandfrei gewährleistet,
- die geforderte Leistung (Produktionsrate) erreicht und
- eine hohe Verfügbarkeit aufweist.
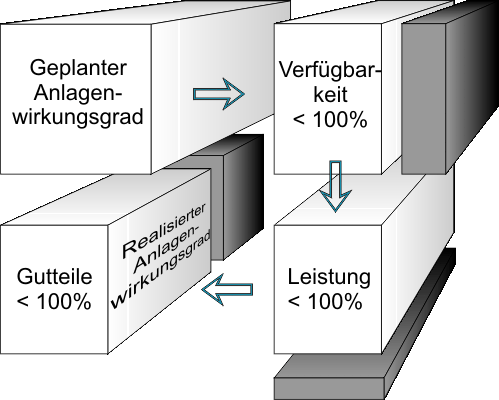
Abb.1: Der geplante Anlagenwirkungsgrad wird durch unzureichende Verfügbarkeit, Produktionsrate und Produktqualität reduziert
Der Kundennutzen lässt sich also zum Beispiel für eine Produktionsanlage durch die Kennzahl Anlagenwirkungsgrad beschreiben (Abb1). Dieser ist ein Maß für die Produktivität der Anlage bezogen auf den Sollwert.
Der Verfügbarkeit der Anlage kommt dabei eine besondere Bedeutung zu, weil einmal verlorene Zeit nicht zu ersetzen ist. Die Verfügbarkeit zu einem Zeitpunkt ist definiert als:
PA = MTBF/(MTBF+MTTR) (1)
Mit:
- MTBF: Mittlere Zeit zwischen zwei Ausfällen (Mean Time Between Failures)
- MTTR: Mittlere Reparaturzeit (Mean Time to Repair)
PA (Point Availability) ist eine Kenngröße des Produktes, in der geplante Abschaltzeiten und die kleinen Probleme des betrieblichen Alltags noch nicht enthalten sind.
Diese berücksichtigt die betriebliche Verfügbarkeit OA (Operational Availability) als weitere wichtige Kennzahl für die Praxis:
OA = MTBMA/(MTBMA+MDT) (2)
Mit:
- MTBMA: Mittlere Betriebszeit zwischen Wartungsarbeiten,geplant und ungeplant (Mean Time Between Maintenance Activities)
- MDT: Mittlere Abschaltzeit (Mean Down Time)
Während die Einflussgrößen Produktionsrate und Produktqualität auch dann, wenn sie nicht 100% erreichen, immer noch eine beherrschte Produktion zulassen, ist Verfügbarkeit die Voraussetzung für eine wertschöpfende Tätigkeit. Weil die Verfügbarkeit durch ungeplante Stillstände reduziert wird, ist die Planung von Gegenmaßnahmen per se mit Unsicherheiten behaftet. Diese wachsen absolut mit dem Defizit an Verfügbarkeit
Ausfälle
Die Zahl der Ausfälle, die in einer Gesamtheit von gleichartigen Einheiten im Zeitraum δt auftritt, wird durch die sogenannte Badewannenkurve (Abb. 2) beschrieben. Diese Kurve ist empirisch und wird durch einfache Modelle nur in ihren Teilbereichen beschrieben.
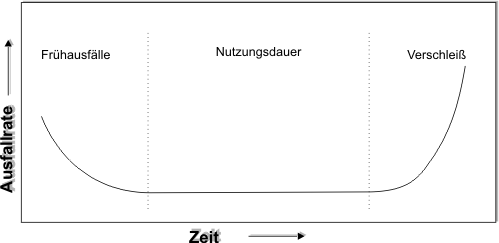
Abb. 2: Ausfallrate als Funktion der Zeit: "Badewannenkurve"
Was lässt sich nun aus dieser Auftragung der Ausfallrate über der Zeit entnehmen?
Mit Hilfe der Steigung der Ausfallrate kann die Kurve in drei Bereiche unterteilt werden.
1. Die Ausfallrate fällt: Frühausfälle
Frühausfälle basieren einerseits auf Fehlern, die bereits bei der Auslieferung des Produktes vorhanden waren. Als Ursachen für Frühausfälle werden gefunden:
- Auslegungsfehler (thermisch, Kriech- und Luftstrecken, EMV)
- Softwarefehler
- Defekte Zulieferteile
- Montagefehler
- Fertigungsfehler
- Materialprobleme
Die Fehler haben ihre Ursache in allen Phasen der Produktentstehung und gelangen durch unzureichende Planung und Prüfung zum Kunden. Da die Fehler durch Ausfall der Produkte eliminiert oder durch Reparatur beseitigt werden, sinkt die Ausfallrate
2. Die Ausfallrate ist konstant: Nutzungsphase
Eine konstante Ausfallrate ergibt sich, wenn in einer Anlage verschiedene Komponenten, deren Lebensdauer kürzer ist, als die Lebensdauer der Anlage, nach und nach ausfallen und wieder repariert werden. Ebenso trägt menschliches Verhalten zur konstanten Fehlerrate bei.
- Fehlbedienung,
- Umgebungsbedingungen nicht eingehalten,
- Wartungsintervalle nicht beachtet
sind Ausfallursachen, die statistisch über die Betriebszeit verteilt auftreten können.
Eine weitere Ursachengruppe sind Ausfälle, die durch statistische Schwankungen in den die Lebensdauer bestimmenden Merkmalen hervorgerufen werden. Ursache dafür sind Streuungen in der Fertigung.
Die Ausfallrate wird durch die Belastung, der ein Produkt ausgesetzt ist, beeinflusst. Beispiele für solche Stressfaktoren sind:
- Temperatur
- Absolute oder relative Feuchte
- Vibration und/oder Schock
- Spannungsspitzen aus dem Netz
Die Ursachen sind einerseits durch angepasste Wartungspläne und Schulung der Mitarbeiter, andererseits durch konstruktive Maßnahmen wie größere Sicherheitsreserven, höherwertige Komponenten und Verminderung der Komplexität zu beeinflussen.
Auch die bei Software häufig geübte Praxis, kleinere Bugs in der laufenden Version nicht zu beheben, führt zu einer konstanten Ausfallrate. Wenn eine fehlerhafte Funktion zufällig angefordert wird, stürzt das Programm ab. Nach einem Neustart beginnt das Spiel von neuem, sofern der Nutzer nicht die Ursachen erkennt und vermeiden lernt.
3. Die Ausfallrate steigt an: Verschleiss
Wenn die spezifizierte Nutzungsdauer der Anlage abgelaufen ist, erreichen zahlreiche Funktionsteile die Grenze ihrer Lebensdauer. Mechanismen sind zum Beispiel:
- Bewegliche Teile (Lager, Zylinder, Kolben, Ventile) verlieren durch Abrieb ihre Funktion.
- Teile mit Dauer- oder Wechselbelastung ermüden (Risswachstum, Kriechen, Fließen).
- Materialien verändern sich (Korrosion, Versprödung, Entfestigung).
Durch die Häufung von Ausfällen sinkt die Verfügbarkeit der Anlage soweit, dass kein geordneter Betrieb mehr möglich ist.
Weil nur in den seltensten Fällen wirklich die Anlage als Gesamtsystem das Ende ihrer Lebensdauer erreicht, bestehen zur Verschrottung gewöhnlich Alternativen wie Recycling von Komponenten Generalüberholung oder Aufrüstung. Zwischen diesen Alternativen muss nach wirtschaftlichen Gesichtspunkten gewählt werden.
Die Lebensdauer einer Anlage wird bei bekannter Belastung durch ihre Konstruktion festgelegt. Ebenso werden durch die Konstruktion die Optionen für eine Verlängerung der Nutzung durch Generalüberholung oder Aufrüstung (Retrofit) gegeben. Diese Entscheidungen werden durch den erwarteten technischen Fortschritt in der jeweiligen Branche und durch die Anlagengröße bestimmt.
Reparaturen
Den Mittelwert der mit einem Ausfall verknüpften ungeplanten Stillstandszeiten bezeichnen wir als MTTR (Mean Time to Repair), mittlere Reparaturzeit.
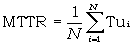 (3)
(3)
Die MTTR ist ein Maß für die Wartungsfreundlichkeit des betrachteten Systems. Da sie als Mittelwert der Zufallsvariablen Tu definiert ist, gehört zu ihrer vollständigen Beschreibung auch eine Streuung, welche die Breite der Verteilung der Reparaturzeiten angibt.
Die Reparaturzeit setzt sich zusammen aus:
- Administration (Meldung des Ausfalls, Entscheidung)
- Diagnose (Hinzuziehen von Spezialisten, Analyse der Ausfallursache)
- Logistik (Reparaturmannschaft bereitstellen, Werkzeuge, Ersatzteile, Dokumentation beschaffen)
- Reparatur (Zerlegen, Austausch defekter Komponenten, Zusammenbau)
- Inbetriebnahme (z. B. Anfahren der reparierten Anlage, Justieren der Betriebsparameter, Verifizieren der Prozessfähigkeit)
Die MTTR wird durch konstruktive Maßnahmen beeinflusst: Die Diagnose wird durch Hilfsmittel (Datenspeicher, On-Line Diagnose) beschleunigt. Durch geschickte Planung der LRU (Lowest Replaceable Unit, Austauscheinheit) und deren Zugänglichkeit wird der Zeitbedarf für die eigentliche Reparatur abgekürzt.
Mindestens gleichgewichtig sind Managementeinflüsse, durch die sichergestellt wird, dass Entscheidungs- Diagnose- und Logistikprozesse nicht mehrfach ablaufen. Wenn Einflüsse, die nicht aus dem Anlagenkonzept resultieren, überwiegen, muss die MTTR durch die MDT (Mean Down Time) ersetzt werden.
Wirtschaftlichkeit
Die Verbesserung der Verfügbarkeit einer Anlage lässt sich ohne Konzeptänderungen gewöhnlich durch finanziellen Aufwand erreichen.
- Die Zahl der Ausfälle kann durch Redundanz, höherwertige Bauteile oder häufigere vorbeugende Wartung reduziert werden.
- Die MTTR kann durch größere LRU, größere Reparaturmannschaften, größere Ersatzteillager und intensivere Schulung der Mitarbeiter abgekürzt werden.
- Die Nutzungsdauer kann durch größere Sicherheitsfaktoren und die Verwendung von höherwertigen Materialien und Komponenten verlängert werden.
Eine Optimierung wird über Wirtschaftlichkeitsbetrachtungen erreicht. Um Produkte zu vergleichen werden die Lebenszykluskosten, LCC berechnet.
Die Lebenszykluskosten LCC setzen sich wie folgt zusammen:
LCC = A + B + W + R (4)
Die zeitabhängigen Kosten werden über die geplante Anlagenlebensdauer akkumuliert.
| Formelzeichen | Bezeichnung | Darin sind enthalten |
| A | Anschaffungskosten |
|
| B | Betriebskosten |
|
| W | Wartungskosten (geplante und ungeplante Wartungen) |
|
| R | Kosten für Recycling bzw. Verschrottung |
|
Die Berechnung der Lebenszykluskosten dient dem Hersteller als Vergleichsmaßstab für Produktvarianten in der Entwicklung. Außerdem sind die Life Cycle Costs ein Verkaufsargument gegenüber dem Kunden. Weil der Kunde sein Kalkulationsschema zum Vergleich der Angebote verschiedener Anbieter verwenden wird, sollte der Hersteller die Schemata seiner Hauptkunden kennen und mit dem eigenen vergleichen.
Sicherheit
Die Gewährleistung der Sicherheit bei menschlichen Fehlhandlungen und bei Defekten der Anlage erfordert häufig zusätzliche Einrichtungen, die zum bestimmungsgemäßen Betrieb der intakten Anlage theoretisch nicht erforderlich sind.
Diese Komponenten erhöhen die Komplexität der Anlage und verringern dadurch ihre Zuverlässigkeit.
Keinesfalls darf die Zuverlässigkeit der Anlage auf Kosten der Sicherheit optimiert werden.
Sicherheit hat Vorrang.
Kundenwünsche verstehen und in eine Spezifikation umsetzen
Weil Zuverlässigkeit als die Fähigkeit, zu einem gegebenen Zeitpunkt die spezifizierten Funktionen zu erfüllen, definiert ist, wird ein Kunde nur dann durch die Zuverlässigkeit eines Produktes zufriedengestellt werden können, wenn die spezifizierten Funktionen präzise vereinbart sind und in vollem Umfang erfüllt werden. Darüber hinaus bestehen bei Endverbrauchern unausgesprochene Erwartungen an die Zuverlässigkeit und Gebrauchsdauer des Produktes.
Wenn der Kunde das Produkt bestimmungsgemäß benutzt, muss es den Output liefern, den er erwartet. Der Hersteller muss aber auch damit rechnen, dass der Kunde in einem gewissen Rahmen vom bestimmungsgemäßen Gebrauch abweicht. Dies sollte einerseits die Sicherheit nicht beeinträchtigen, andererseits auch nicht zu unverhältnismäßigen Verlusten führen.
Das Produkt, das im Angebotsprozess definiert wird, wird nach der Übergabe an den Kunden von dessen Personal eingerichtet, programmiert, bedient, genutzt und gewartet. Unter Personal kann dabei auch ein Dienstleister zu verstehen sein, den der Kunde beauftragt. Dadurch werden Mensch-Maschine-Schnittstellen aktiviert .
Weil für menschliche Aktionen keine detaillierten Spezifikationen sondern nur Akzeptanzgrenzen festgelegt werden können, ist ein System, das den Menschen einschließt im technischen Sinne nicht determiniert (La Mettrie zum Trotz). Hier kommt es darauf an, die Maschine und ihre Benutzeroberfläche so zu gestalten, dass es dem Menschen leicht fällt den Auftrag, den er mit der Maschine ausführen will, in eine korrekte Eingabe umzusetzen.
Die Maschine selbst ist determiniert. Sie liefert, sofern sie intakt ist, auf korrekte Eingaben hin spezifikationsgemäße Ausgaben (Abb. 4). Zu den Eingaben zählen natürlich nicht nur die unmittelbaren menschlichen Aktionen und Steuerungssignale, sondern auch die Umgebungsbedingungen.
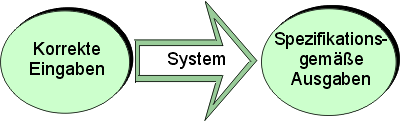
Abb. 4: Die intakte Maschine als System
Die klare Definition der Eingaben und Ausgaben ist unabdingbare Voraussetzung für den Bau und die Nutzung eines zuverlässigen Produktes. Daher kommt ihrer einvernehmlichen Festlegung entscheidende Bedeutung zu.

Abb. 5: Die defekte Maschine muss auf die möglichen Eingaben mit sicheren Ausgaben reagieren.
Weiterhin muss aber damit gerechnet werden, dass
- die Eingaben nicht korrekt sind und dass
- das Produkt defekt ist.
Damit ergeben sich Ausgaben, die nicht zu den in Abb. 4 definierten spezifikationsgerechten Ausgaben gehören. Von diesen Werten ist zu fordern, dass sie zur Menge der sicheren Ausgaben gehören (Abb. 5). Jedes Fehlerbild der Maschine erzeugt prinzipiell einen eigenen funktionalen Zusammenhang zwischen den möglichen Eingaben und den Ausgaben. Diese sind in Abb. 5 zusammengefasst.
Der Bereich der möglichen Eingaben kann nicht unendlich sein, sondern muss dadurch begrenzt werden, dass Eingaben als nahezu unmöglich ausgeschlossen werden. Ebenso müssen die sicheren Ausgaben definiert werden, weil Sicherheit in den Grenzbereichen eine Frage der Akzeptanz ist. Auch diese Punkte müssen während des Angebotsprozesses mit dem Kunden geklärt werden. Durch eine weitgehende Normung der Forderungen wird diese Klärung sehr vereinfacht. Sie ist trotzdem erforderlich.
Design für Zuverlässigkeit und Wartungsfreundlichkeit
Die Ergebnisse des Angebotsprozesses
- festgelegter Eingabebereich für zuverlässigen und sicheren Betrieb der Anlage,
- festgelegter Bereich für spezifikationsgerechte und sichere Ausgaben und
- Verpflichtung des Herstellers zu festgelegten Kosten und in einem festgelegten Zeitrahmen ein System zu realisieren, das den Eingabebereich auf den Ausgaberaum abbildet,
werden im Entwicklungsprozess in eine konkrete Beschreibung des Produktes umgesetzt.
Der Ausdruck Entwicklungsprozess soll sich sowohl auf die Entwicklung eines neuen Produktes als auch auf die Planung einer Anlage nach Kundenspezifikation beziehen. Die Aufgaben unterscheiden sich in ihrer Komplexität, arbeiten aber im Prinzip mit identischen Lenkungsinstrumenten und Modellen.
Weil in der relativ kurzen Entwicklungsphase die Life Cycle Costs, die insgesamt ein mehrfaches der Anschaffungskosten ausmachen können, weitgehend festgelegt werden, ist diese Phase für die Zufriedenheit des Kunden von erheblicher Bedeutung. Als Managementinstrument zur Sicherstellung des Erfolges der Entwicklungstätigkeit hat sich die Strukturierung des Entwicklungsprozesses nach Phasen, die mit einem Review, einer formellen Designprüfung, abgeschlossen werden, bewährt. Die einzelnen Phasen umfassen spezifische Tätigkeiten aus den Bereichen
- Projektmanagement,
- Technische Entwicklung,
- Qualitätsmangement,
- Controlling,
- Beschaffung und, last not least,
- Vertrieb.
Der Leitung obliegt die Aufgabe auf der Basis der Reviewergebnisse über die Fortführung des Projektes und die Freigabe der Mittel für die nächst Phase zu entscheiden.
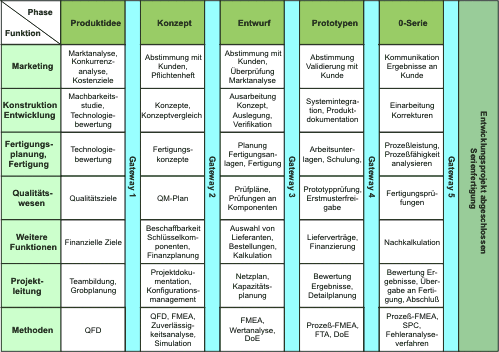
Strukturierung des Entwicklungsprozesses wird durch Normen und branchenspezifische Forderungen zum Qualitätsmanagement (ISO 9001, ISO/TS 16949) vorgegeben. Die detaillierte Gestaltung des Prozesses ist Aufgabe der jeweiligen Organisation. Abbildung 6 zeigt einen Vorschlag für eine grobe Struktur mit den der jeweiligen Phase zugeordneten Aufgaben gegliedert nach den Tätigkeitsbereichen. Unabhängig von einer detaillierten Formulierung von Phasen, deren Inhalten und den Gateways, die ein Projekt passieren muss, sind
- die Zusammenarbeit der Funktionen im Unternehmen,
- die Einbeziehung der Kunden und
- die frühzeitige Zusammenarbeit mit Lieferanten für Teile und Fertigungseinrichtungen
wesentlich für eine hohe Erfolgswahrscheinlichkeit bei der Realisierung des Projektes. Die Phasen Produktidee und Konzept überlappen sich mit dem Angebotsprozess. Dort stellen sie den technischen Beitrag zur Erstellung des Angebots dar.
Gateways werden passiert, wenn die Übereinstimmung des Projekts mit den Zielen für die durchlaufene Phase nachgewiesen ist. Passieren eines Gateway bedeutet auch Freigabe der nächsten Phase. Dadurch laufen sowohl der Verbrauch von Mitteln als auch die Festlegung von Life Cycle Costs kontrolliert ab. Der Soll-Ist-Vergleich wird zumindest bei größeren Projekten in einer formellen Entwurfsprüfung, einem Design-Review, durchgeführt.
Neben einer geeigneten Konstruktionsmethodik (Design to X, X = Cost, Manufacturing, Assembly, Repair, Recycling, ...) sind Quality-Engineering (QE)-Methoden erforderlich, um die geforderte Zuverlässigkeit zu realisieren. Zu nennen sind hier:
- FMEA
- Zuverlässigkeitsanalyse
- Versuchsplanung und Zuverlässigkeitstests
- Datenanalyse
Planung der Zuverlässigkeit setzt voraus, dass wir für unser System ein Rechenverfahren finden, das es uns erlaubt, den Wert der Zuverlässigkeitsfunktion R(t) zu jedem beliebigen Zeitpunkt t innerhalb der geplanten Nutzungsdauer anzugeben. Weil eine Maschine prinzipiell ein deterministisches System ist, könnte man bei bekannten Ausgangsbedingungen und Betriebsbedingungen eine Prognose für alle Komponenten rechnen. Dies scheitert jedoch an der mangelnden Verfügbarkeit und Kontrollierbarkeit der notwendigen Daten und an der Größe des Problems. Daher ist eine statistische Behandlung des Problems erforderlich. Die Zeit bis zum ersten Ausfall, oder bei reparierbaren Systemen die Zeit zwischen zwei Ausfällen, ist eine Zufallsvariable. Uns interessieren die Verteilungsfunktion, welche die Wahrscheinlichkeit für das Auftreten einzelner Werte angibt, und die Parameter, die Lage und Verteilungsbreite der Funktion bestimmen.
Ein Zuverlässigkeitsmodell lässt sich mit relativ geringem rechnerischen Aufwand auf der Basis der Annahme statistisch unabhängiger Ausfälle von Komponenten und konstanter Ausfallraten erstellen. Für serielle Strukturen (alle Komponenten müssen intakt sein, damit das System intakt ist) ergibt sich die mittlere Lebensdauer eines Systems mit n Komponenten (MTTF: Mean Time to Failure) zu:
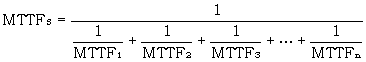 (5)
(5)
Sofern durch Reparatur ein Zustand "wie neu" erreicht wird, können die MTTF durch MTBF ersetzt werden. Stellt man den Zusammenhang zu Ausfallraten her, ist für konstante Ausfallraten die MTTF (MTBF) gleich 1/Ausfallrate. Damit gelangen wir zu der bekannten Formel:
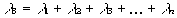 (6)
(6)
Offensichtlich liefern nicht alle Komponenten Beiträge zu allen Funktionen eines komplexen Produkts. Daher sieht die Funktionsanalyse eines Produktes für jede betrachtete Funktion anders aus. Zu einer differenzierten Betrachtung der Zuverlässigkeit eines Produktes werden wir also für jede wichtige Funktion eine Funktionsanalyse erstellen und feststellen, welche Komponenten des Produktes zu dieser Funktion beitragen und welche Beziehungen unter den Komponenten bestehen. Dabei interessiert uns besonders die Frage, ob die betrachtete Funktion des Produktes unbedingt vom Funktionieren der Komponente abhängt, oder ob die Funktion auch dann noch vorhanden ist, wenn die Komponente ausgefallen ist. Ausgehend von der Funktionsanalyse erstellen wir nun ein Zuverlässigkeits-Blockdiagramm (Abb. 7).
Dazu betrachten wir die Systemelemente auf einer Ebene und fragen: Ist der Funktionsbeitrag des Systemelementes für die betrachtete Funktion des Produktes absolut erforderlich oder nur bedingt erforderlich? Elemente, deren Funktion absolut erforderlich ist schalten wir im Zuverlässigkeits-Blockdiagramm in Reihe. Wenn die Funktion bedingt erforderlich ist, schalten wir das Systemelement mit den Elementen, die die Funktion auch übernehmen können, parallel und diese Parallelschaltung, von der eine gegebene Anzahl von Pfaden intakt sein muss, in Reihe mit den übrigen Elementen.
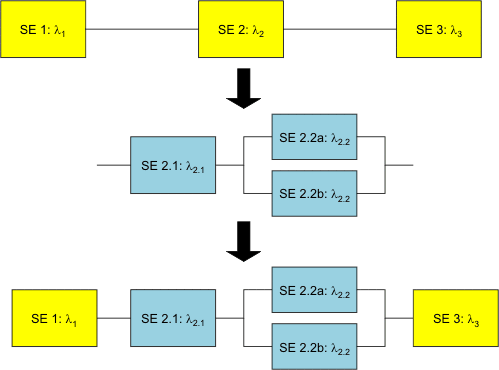
Abb. 7: Zuverlässigkeitsmodelle können aus der Systemstruktur entwickelt werden. Die Ausfallrate eines Systems erhält man aus der Addition der Ausfallraten der Komponenten. Redundante Parallelsysteme werden gesondert berechnet.
Das System aus Abb. 7 hat also die Systemausfallrate λ S=λ1+λ2+λ3. Das Systemelement 2 ist durch Reihenschaltung des Elements 2.1 mit der Parallelschaltung der Elemente 2.2a und 2.2b aufgebaut, die beide die Ausfallrate λ2.2 haben.
Für redundante Strukturen mit parallelgeschalteten Elementen ist die Ausfallrate nicht konstant, auch wenn die einzelnen Komponenten konstante Ausfallrate haben. Dies entspricht dem Sinn der Redundanz, durch die ja mindestens für kurze Betriebszeiten eine reduzierte Ausfallrate erreicht werden soll. In diesem Fall ist daher eine detailliertere Berechnung erforderlich Wenn wir davon ausgehen, dass die Systemelemente 2.2a und 2.2b baugleich sind und eine 1 aus 2 Redundanz bewirken, beträgt die MTTF:
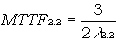 (7)
(7)
Für das gesamte Systemelement 2 ergibt sich:
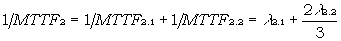 (8)
(8)
Und damit für das Gesamtsystem:
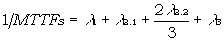 (9)
(9)
Dies ist die Basis der beispielsweise bei der Entwicklung elektronischer Geräte häufig angewendeten Parts-Count-Methode. Berücksichtigt man noch den Einfluss der Betriebsbedingungen auf die Ausfallraten der einzelnen Komponenten (Parts-Stress), gelangt man zu Abschätzungen, die sich mindestens für den Vergleich von Design-Varianten als recht brauchbar erwiesen haben.
Trotz des Erfolges des Modells auch für mechanische Konstruktionen ist es offensichtlich, dass eine Reihe von Fragestellungen unbeantwortet bleibt.
Mindestens wenn in dem betrachteten System Hardware und Software gemeinsam das Ausfallverhalten bestimmen, müssen mögliche Ausfälle durch Softwarefehler berücksichtigt werden. Diese sind von Anfang an vorhanden, führen aber erst dann, wenn die fehlerhafte Funktion der Software angefordert wird, zum Ausfall. Das Zuverlässigkeitsmodell muss also durch ein additives Glied λ S* erweitert werden. Dieses bezeichnet die Ausfallrate, die durch systematische Fehler verursacht wird. Für eine Software, die in verschiedenen Installationen mit unterschiedlichen Operationsprofilen betrieben wird, ergibt sich der in Abb. 8 dargestellte prinzipielle Verlauf der Zuverlässigkeitsdaten, wenn Bugs nach einem Ausfall mit einer Reparaturrate µ=1/MTTR behoben werden.
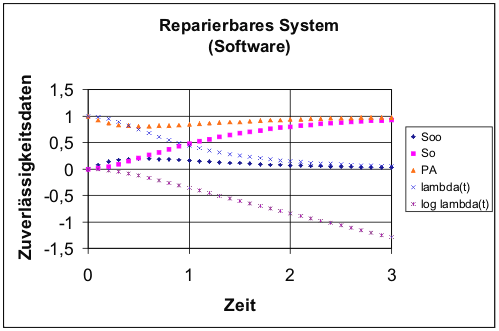
Abb. 8: Zahlenbeispiel zur Zuverlässigkeit eines reparierbaren Systems mit drei Zuständen S0, intakt, S1, defekt, und S∞, ausgefallen.
Für die Rechnung in Abbildung 5.9 wurden die folgenden Werte verwendet:
S0(0) = 0, S1(0) = 1, λ j* = 1, μ = 3
Die Besetzung des defekten Zustandes S1 zur Zeit 0 ist 1, weil alle Installationen zu Anfang fehlerhaft sind. Durch Reparatur ausgefallener Systeme wird zunehmend der intakte Zustand S0 besetzt. Dadurch verbessert sich langfristig die Verfügbarkeit PA.
Das Verhalten bei langen Zeiten wird durch die Ausfallrate bestimmt, während die Reparaturrate die Besetzung von S∞ bei kurzen Zeiten steuert. Weil sich die Ausfallrate des Systems λ(t) auf die Anzahl der nicht ausgefallenen Einheiten bezieht, ist sie nicht konstant, sondern fällt nach einer durch µ bestimmten Anlaufzeit ab. Nach der Anlaufphase stellt sich im halblogarithmischen Maßstab ein linearer Abfall der Ausfallrate mit der Steigung -0,5 ein. Dieses Verhalten auch in der Praxis beim Testen von Software gefunden. Es stellt eine Basis für die Extrapolation von Ausfallraten dar.
Über die Ausfälle von Software bei Tests sollten daher von Anfang an Aufzeichnungen geführt werden. Diese dienen als Grundlage für
- die Abschätzung des erforderlichen Testaufwandes, um ein vorgegebenes Zuverlässigkeitsniveau zu erreichen,
- die Optimierung des Testaufwandes bei Kenntnis der Prüfkosten pro Zeiteinheit und der Kosten für die Bearbeitung von Reklamationen und
- die Beurteilung des Testerfolges. Sehr langsame Verbesserung deutet auf ineffiziente Test- und/oder Reparaturmethoden hin.
Systematische Hardwarefehler verhalten sich analog. Daher ist es sinnvoll für ein komplexes System, wenn systematische Fehler nicht ausgeschlossen werden können, die gesamte Ausfallrate λG als Summe der durch zufällige und durch systematische Fehler verursachten Ausfallraten zu schreiben.
λG = λS + λS* (10)
λS und λS* setzen sich entsprechend dem gewählten Zverlässigkeitsmodell aus den Ausfallraten der Systemkomponenten zusammen.
Ständige Verbesserung
Betriebsdauern einer Anlage von mehreren Jahren bis zu mehreren Jahrzehnten machen eine aktive Zusammenarbeit von Hersteller und Kunde zur Verbesserung der Zuverlässigkeit der Anlage erforderlich. Für den Hersteller dient dies einerseits zur Reduzierung der Garantiekosten. Andererseits ist es ein Feldversuch, aus dem er verläßliche Daten zur tatsächlichen Zuverlässigkeit der Anlage und zur Wirksamkeit von Verbesserungsmaßnahmen ziehen kann. Der Betreiber der Anlage erreicht durch die Eliminierung von Fehlerquellen eine Verbesserung der Lebenszykluskosten.
Dieser ständige Verbesserungsprozess besteht aus den Schritten:
- Sammeln und Auswerten von Daten,
- Setzen von Zielen,
- Festlegen von Maßnahmen,
- Durchführen der Maßnahmen und
- Kontrolle der Wirksamkeit
Dies entspricht den Standardforderungen an einen kontinuierlichen Verbesserungsprozess.
Dabei sind zwei Phasen zu unterscheiden:
- Garantiezeit und
- Betrieb nach der Garantiezeit
Weil Ausfälle in der Garantiezeit unmittelbar mit Kosten für den Hersteller verbunden sind, wird er in dieser Phase alle Ausfälle analysieren, um die Ursachen zu finden und zu eliminieren. Ein statistische Auswertung gibt Hinweise auf die Notwendigkeit spezieller Maßnahmen zur Reduzierung von Frühausfällen und auf die nach Beseitigung der Ursachen für Frühausfälle zu erwartende Zuverlässigkeit (Reliability Growth).
Nach der Garantiezeit hat der Nutzer die führende Rolle bei der Verbesserung der Zuverlässigkeit der Anlage. Für den Hersteller ist eine aktive Beteiligung an den Programmen des Nutzers sinnvoll, weil dies
- dem Hersteller eine Datenbasis für die Verbesserung seiner Zuverlässigkeitsmodelle bringt,
- Erfahrungen zu menschlichem Fehlverhalten vermittelt, die zur Verbesserung der Mensch-Maschine-Schnittstelle und der Schulung führen, und
- die Kundenzufriedenheit verbessert.
Auf dieser Seite
- Methoden zur Planung von Zuverlässigkeit und Wartungsfreundlichkeit
- Abkürzungen und Definitionen
- Software, Standards, Leitfäden
Abkürzungen, Definitionen
- Anlagenwirkungsgrad:
- OEE=PA*R*Q*100 Die Verfügbarkeit PA, die Produktionsrate R und der Anteil der Gutteile Q werden dabei als Bruchteile bezogen auf den Sollwert angegeben. Die Verfügbarkeit bezieht sich dabei auf die Nettozeit
- Ausfall:
- Beendigung der Fähigkeit einer Einheit ihre spezifizierte Funktion zu erfüllen
- Austauscheinheit (LRU, Lowest Replaceable Unit):
- Kleinste Einheit, die bei einem Ausfall ausgetauscht, gegebenenfalls im Werk repariert und danach wieder als Ersatzteil zur Verfügung gestellt wird.
- Ausfallrate:
- λ(t) = - 1/R(t) * dR(t)/dt Die Ausfallrate gibt die Geschwindigkeit an, mit der eine gegebene Zuverlässigkeit R zum Zeitpunkt t abnimmt
- Betriebszeit:
- Betriebszeit = Nettozeit - Ungeplante Abschaltzeit
- Nettozeit:
- Nettozeit = Gesamte verfügbare Zeit - Geplante Abschaltzeit
- Verfügbarkeit:
- PA(t)=MTBF/(MTBF+MTTR) Die Verfügbarkeit ist die Wahrscheinlichkeit, dass ein System seine spezifizierte Funktion zu einem Zeitpunkt t erfüllt. Die Verfügbarkeit verknüpft die Kennzahlen für die Zuverlässigkeit (MTBF, Mean Time Between Failures) und die Wartungsfreundlichkeit (MTTR, Mean Time To Repair).
Software, Standards, Leitfäden
- Software für Zuverlässigkeitsplanung
- Relex
- Item
- ReliaSoft
- Handbücher, Datensammlungen
- The Reliability Information Analysis Center The Reliability Information Analysis Center (RIAC) is the Department of Defense (DoD) chartered Center of Excellence in the fields of Reliability, Maintainability, Quality, Supportability, and Interoperability.
- SAE: Standards und Guidelines für Zuverlässigkeit und Wartungsfreundlichkeit im Automobilbau.
- Standards
- VDI: VDI 3423, Verfügbarkeit von Maschinen und Anlagen. Die Richtline gibt Definitionen zu Ausfall- und Nutzungszeiten von Maschinen und Anlagen. Sie enthält weiterhin Hinweise f$uuml;r die Erfassung von Ausfallzeiten.
- DIN: DIN EN 60300 1 - 3, deutsche Fassung der IEC-Normen zum Zuverlässigkeitsmanagement. Managementsysteme, Erhebung von Daten, Leitfaden zur Anwendung usw.

 QM-SYSTEME
QM-SYSTEME